Sunday, May 6
7:10 am
It is +4 °C, with a high forecast of +13 °C.
From the Environment Canada website:
Today Clearing this morning. Wind northwest 40 km/h gusting to 60 diminishing to 20 near noon. High 13. UV index 6 or high.
Tonight Clear. Low minus 3.

7:30 am Musings
There are only a few patches of snow left from yesterday's weather. It should all be gone soon. Positive temperatures do that to the snow. Yesterday was almost 15 degrees below normal for this time of year. Today will be close to normal. But we will keep the bedding plants in the garage until Tuesday.
I am normal for this time of day. The hot coffee is beside my right hand.
With the wintery weather yesterday, I stayed low and indoors. Thus no weight training, no coulee walk. But a day off once in awhile is not a bad idea. The important point is to not extend the break. The LFC is open from 10:00 am - 6:00 PM on Sunday.
8:00 am Literature

I have selected The Song of Achilles as my next novel to read. It is an attempt to rework The Illiad into novel form.

7:30 am Mathematics

I have yet to re-open Gilbert Strang's textbook "Introduction to Linear Algebra". It is time to try this again. One of the best features of this is that there is also a complete set of video lectures of Strang giving a course at MIT based on this book.
Linear Algebra, as I understand it, is a specialized subset of Modern/Abstract Algebra. The focus in on vectors and matrices and their manipulations. There is virtually no mention of Groups, Rings and generalized algebras.
Once again, it is difficult to quickly and easily to describe the activities involving vectors and matrices on a web page.
I have had a quick look at a software program called Maple which is recognized as an excellent software package for visualizing mathematical topics but it cost about a thousand dollars. Not really viable for an individual. Back to the text.

Me: Let's begin with chapter 1 Introduction to Vectors.
Strang: Chapter 1 Introduction to Vectors [p. 1 - 30]
1.1 Vectors and Linear Combinations [p. 2 - 10]
There are 3 ways to represent a vector: as two numbers, as an arrow from (0, 0), and as a point on a plane.
Me: As I understand it, linear algebra is thinking about how vectors and combinations of vectors appear in a space of 2, 3 or more dimensions. It is surprising to see a book such as Strangs' and realize that this thick tome is all about just this. Notation is a critical feature of the topic.
Strang: A vector can be represented as a column of 2 numbers, with square brackets around them. Or it can be represented as a row vector like this: (2, 3). It can also be represented as an arrow from (0, 0), or as a point in the plane.
Me: I recall using a computer language called APL when I was a graduate student. Its strength was the capability to manipulate vectors and matrices. I have this on my Mac. Now to see if it is easy to embed the use of APL within this web page.
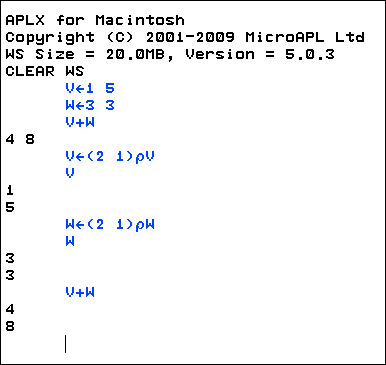
This took a few minutes as I wanted a border around the screen capture. This involved a google search and then downloading a 30-day trial version of Snagit. I like this. But I will play with the trial for a few days before purchasing it.
I have been mulling over this idea of the representation of a vector for the last couple of hours. At an abstract level a vector is an idea, a concept. We usually represent ideas (concepts) by means of language. Thus a vector may also have length and direction (relative to a coordinate axis). If there is more than one vector then one can explore various possible relationships among them. This may be interesting, or not. However the ideas may also have utility. They may contribute to the solution of real-world problems. Engineering and economics are two areas where these ideas are particularly useful.
The title of the book is Linear Algebra. Thus the book focuses on linear relationships. It is possible to imagine non-linear relationships as well, but this is (apparently) better left for another day (book).
Strang: He identifies 3 questions as being important:
- What is the picture of all combinations cu ? The answer is that the combinations fill a line.
- What is the picture of all combinations cu + dv ? The combinations fill a plane. (i.e. all possible combinations of 2 vectors)
- What is the picture of all combinations cu + dv + ew ? The combination fills a three-dimensional space.
Me: I like this. Right at the outset we are imagining situations that involve all numbers, not just particular examples.
Strang: The next example is a problem. Given three vectors, each with 2 elements, find a linear combination of the first two vectors that gives the third vector.
Me: This is more easily expressed in a conventional (hand-written) notation than in a web page. For me, I can easily switch to a (fountain) pen & paper, but in general it raised the complex issue of developing a notation that permits one to utilize the power of the computer. Two software programs that come to mind that do this are Mathematica and Maple. Unfortunately both are prohibitively expensive for an individual. Thus mathematics is biased in favor of the rich. This is a new cultural development! In the past a pad and a pencil opened the doors to anyone so inclined. Now emath favors a small subset of the general population.
Me: There are a series of exercise on pages 8 - 10, but I have done some of these before and feel that I can proceed to the next section without difficulty.
Strang: 1.2 Lengths and Dot Products [p. 11 - 21]
The previous section described how to add (or subtract) any two (or more) vectors. This section is about multiplying vectors. There are many ways that one can imagine doing this. The trick is to come up with ways that are in some sense interesting and/or useful. One such way is called the dot product (also called the inner product).
Take two vectors with the same number of elements. Multiply each pair of numbers. Then add all of these products to create a single number. That number is called the dot product.
Me: Let's try this using APL.
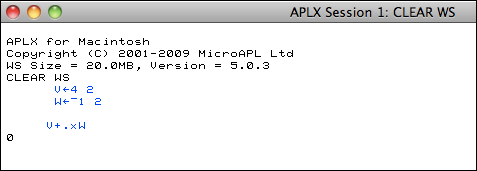
Note that I have created 2 vectors V and W and assigned 2 values to each vector. The notation in APL for computing the dot product is 3 symbols +.x . This is read from right to left: first multiply all of the corresponding elements, then add all of these intermediate products. The result in this case is zero. I really like the mnemonic value of the plus-dot-times symbol.
Strang: When the dot product is zero, this indicates that the two vectors are perpendicular (i.e. orthogonal) to each other. This is another way of saying that the two vectors are independent.
Now consider the dot product of a vector with itself.
The result turns out to be the square of the length of the vector. Think of Pythagorus' Theorem.
That is, the length of a vector is the square root of the dot product of a vector with itself.
The unit vector is the vector divided by its length.
The cosine of the angle between two vectors is the dot product divided by the product of the two lengths.