Tuesday, April 24
6:50 am
It is +11 °C, with a high forecast of +26 °C.
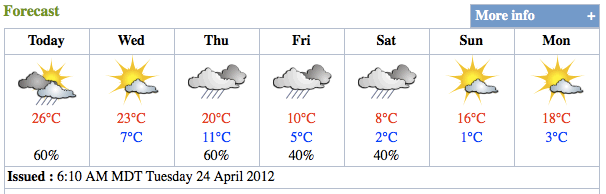
From the Environment Canada website:
Today Cloudy with 60 percent chance of showers this morning then a mix of sun and cloud. Wind becoming west 50 km/h gusting to 70 near noon. High 26. UV index 6 or high.
Tonight Clear. Wind west 30 km/h becoming light near midnight. Low 7.
7:40 am Musings
This is a good time for a quick review of my activities:
- Birding: I should have a look at a few spots such as Henderson Lake and Picture Butte to see if there are wildfowl. I also want to review my exposure settings - I would like to try setting the exposure time to something like 1/100 sec and see if that prevents blurring due to motion.
- Cooking: Hopefully the book "The Free Range Cook" will arrive before the end of the month. I want to make a batch of granola with rolled oats instead of steel-cut oats so I can compare the two.
- Geocaching: I would like to make a trip to the Crowsnest Pass to look for a few caches. This would give me an opportunity to check the condition of the campground at Chinook Lake as well. I am curious to see if it is open and if the snow has melted.
- Life: I want to begin using the facilities at a fitness center.
- Literature: This needs improving. The Perlman novel is my top priority.
- Mathematics: I have just begun this. Now to keep it up!
- Musings: Okay.
- Technology: I am vacillating between buying a MacBook Air and a MacBook Pro. Both models are due for an upgrade so it makes sense to hold off for a bit.
- Trains: Next task is to finish building the viaduct model.
There is a light drizzle at the moment. The smell of fresh cool air is a delight in the morning.
8:30 am Mathematics

Me: The air is fresh this morning. Ideal for mathematics. Continuing the first chapter of Pinter's "A Book of Abstract Algebra".
Pinter: "We must carefully note that the axiomatic method is not a way of discovering facts but of organizing them. New facts in mathematics are found, as often as not, by inspired guesses or experienced intuition. To be accepted, however, they should be supported by proof in an axiomatic system. [p. 12]
Me: True enough. But for most of us, the issue is not creating new math but deeply understanding whatever math we wish to use.
Pinter: "We choose to ignore the properties of the actual objects in a system of algebra (they may be numbers, or matrices, or whatever - we disregard what they are), and we turn our attention simply to the way they combine under the given operations." [p. 13]
Me: This is the heart of the matter. Algebra is a study one level removed from the actual objects that are particular exemplars of what is being studied.
Pinter: "... mathematicians slowly discovered that all the algebraic laws which hold in any system can be derived from a few simple, basic ones. This is a genuinely remarkable fact, for it parallels the discovery made by Euclid that a few very simple geometric postulates are sufficient to prove all the theorems of geometry.
Me: Why is this so? Why are the algebraic laws derivable from a few basic ones? I want to return to this later.
Pinter: "... when a mathematician nowadays speaks of a ring, the mathematician is referring to a set A with two operations, usually symbolized by + and . , having the following axioms: Addition is commutative and associative, it has a neutral element commonly symbolized by 0, and every element has an inverse -a with respect to addition. Multiplication is associative, has a neutral element 1, and is distributive over addition. ... Matrix algebra is an example of a ring ... there are many other examples of rings rings of numbers, rings of functions, rings of code 'words', rings of switching components, and a great many more." [p. 15]
Me: Got it. A ring is any set with 2 operations that satisfy a few basic axioms.
Pinter: "Nature presents us with a myriad of interwoven facts and sensations, and we are challenged at every instant to single out those which are immediately relevant and discard the rest. ... Nature is not made up of forces, velocities, and moments of inertia. Nature is a whole - nature simply is! The physicist isolates certain aspects of nature from the rest and finds the laws which govern these abstractions. It is the same with mathematics." [p. 16]
Me: Got it, again.
Pinter: "The movement toward axiomatics and abstraction in modern algebra began about the 1830s and was completed 100 years later." [p. 17]
Me: The 1830s were the time of Abel and Galois. But why does Pinter say that the task (of providing the axiomatic basis for algebra) was completed? Surely new systems will continue to be created and explored.
This completes Chapter One.
5:30 PM Life
I am pushing forward. I have now set up an appointment on Thursday with a trainer at the Lethbridge Fitness Center to begin a program of exercises. This will be a new adventure for me. I am already thinking of what tattoo I should have first. My coulee walks have been steady - I have not missed a day since I began a week ago. I am keeping a daily record of my eating and am trying to keep it close to 1200 cal/day. The overall goal is to lose 2 pounds/week. So far so good, but it is early.