May 12, 6:30 am Mathematics

I am leaning toward a study of Groups rather than Linear Algebra, although I would like to keep my finger in both. I also find the Ash & Gross book more friendly than the Pinter book.
Chapter 2 Groups
Ash: "Mathematical sets can be very interesting and easy to define, but very hard to understand in detail. ... If a set can be endowed with extra structure, it can help our understanding. One very common kind of extra structure is a 'composition law' that turns the set into a group. The definition of a group is the most common way mathematicians have of formalizing the concept of symmetry." [p. 13]
Me: This is a perfect opening statement. The emphasis is on understanding and concepts, not algorithms and procedures.
Ash: "SO(3) stands for 'special orthogonal group in three dimensions." [p. 13]
Me: This is not a notation for manipulation, but simply a shorthand for describing a label. It represents the group consisting of rotations of a sphere.
Ash: "A group is a set along with a rule that tells how to combine any two elements in the set to get another element in the set. We usually use the word composition to describe the act of combining two elements of the group to get a third." [p. 14]
Me: This is a clear beginning.
Ash: "The key point about a group is the combination of any two elements to get a third." [p. 15]
Me: I like the emphasis.
Ash: "DEFINITION: A group G is a set with a composition defined on pairs of elements, as long as three axioms hold true:
- There is a neutral element e in G, so that x o e = e o x = x no matter what element of the group is substituted for x.
- For any element x of G, there is some element y in G so that x o y = y o x = e
- For any three elements x, y, and z in G, we have (x o y) o z = x o (y o z) " [p. 17]
Me: This notation may seem unnecessary at first, particularly the use of the small circle o to represent any operation, but this notation gives one the power to manipulate symbols without having to use language to describe what one is doing.
Ash: The group SO(3) is a mathematical idealization which can be used in certain circumstances to describe the rotation of the earth. This is an example of a mathematical idealization, where we ignore slight discrepancies such as the earth is not perfectly spherical. "It pays to ignore these things for our purposes, because if we included every bump on every log we would never see the forest for the trees. That is, we would not see any patterns that repeat. ... We could never see the regularities to abstract from the welter of reality. Mathematics would never be born." [p. 18]
Me: This is rarely made explicit, yet it lies at the heart of not only mathematics but psychology. A concept is an idealization. The concept of a cat is an idealization of all existing cats. This is the very essence of thinking.
Ash: "Any actual rotation should be buildable by integrating some infinitesimal rotation. This is the germ of the theory of Lie groups and Lie algebras, named for the Norwegian mathematician Sophus Lie (pronounced 'lee'). .. A group such as SO(3) hat has infinitesimal generators is called a continuous group. The other main type of group is called a discrete group. ... An example of a discrete group is the set of integers, where we 'compose' two integers by adding them together." [p. 19]
Me: This ends the second chapter. It is devoted totally to ideas, and simple ones at that. There is no actual manipulation of symbols to see what happens. First comes the idea. Using the idea comes second.
May 6, 7:30 am Mathematics

I have yet to re-open Gilbert Strang's textbook "Introduction to Linear Algebra". It is time to try this again. One of the best features of this is that there is also a complete set of video lectures of Strang giving a course at MIT based on this book.
Linear Algebra, as I understand it, is a specialized subset of Modern/Abstract Algebra. The focus in on vectors and matrices and their manipulations. There is virtually no mention of Groups, Rings and generalized algebras.
Once again, it is difficult to quickly and easily to describe the activities involving vectors and matrices on a web page.
I have had a quick look at a software program called Maple which is recognized as an excellent software package for visualizing mathematical topics but it cost about a thousand dollars. Not really viable for an individual. Back to the text.

Me: Let's begin with chapter 1 Introduction to Vectors.
Strang: Chapter 1 Introduction to Vectors [p. 1 - 30]
1.1 Vectors and Linear Combinations [p. 2 - 10]
There are 3 ways to represent a vector: as two numbers, as an arrow from (0, 0), and as a point on a plane.
Me: As I understand it, linear algebra is thinking about how vectors and combinations of vectors appear in a space of 2, 3 or more dimensions. It is surprising to see a book such as Strangs' and realize that this thick tome is all about just this. Notation is a critical feature of the topic.
Strang: A vector can be represented as a column of 2 numbers, with square brackets around them. Or it can be represented as a row vector like this: (2, 3). It can also be represented as an arrow from (0, 0), or as a point in the plane.
Me: I recall using a computer language called APL when I was a graduate student. Its strength was the capability to manipulate vectors and matrices. I have this on my Mac. Now to see if it is easy to embed the use of APL within this web page.
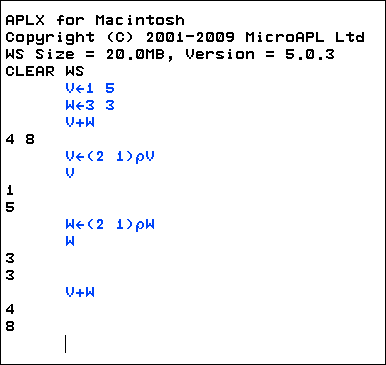
This took a few minutes as I wanted a border around the screen capture. This involved a google search and then downloading a 30-day trial version of Snagit. I like this. But I will play with the trial for a few days before purchasing it.
I have been mulling over this idea of the representation of a vector for the last couple of hours. At an abstract level a vector is an idea, a concept. We usually represent ideas (concepts) by means of language. Thus a vector may also have length and direction (relative to a coordinate axis). If there is more than one vector then one can explore various possible relationships among them. This may be interesting, or not. However the ideas may also have utility. They may contribute to the solution of real-world problems. Engineering and economics are two areas where these ideas are particularly useful.
The title of the book is Linear Algebra. Thus the book focuses on linear relationships. It is possible to imagine non-linear relationships as well, but this is (apparently) better left for another day (book).
Strang: He identifies 3 questions as being important:
- What is the picture of all combinations cu ? The answer is that the combinations fill a line.
- What is the picture of all combinations cu + dv ? The combinations fill a plane. (i.e. all possible combinations of 2 vectors)
- What is the picture of all combinations cu + dv + ew ? The combination fills a three-dimensional space.
Me: I like this. Right at the outset we are imagining situations that involve all numbers, not just particular examples.
Strang: The next example is a problem. Given three vectors, each with 2 elements, find a linear combination of the first two vectors that gives the third vector.
Me: This is more easily expressed in a conventional (hand-written) notation than in a web page. For me, I can easily switch to a (fountain) pen & paper, but in general it raised the complex issue of developing a notation that permits one to utilize the power of the computer. Two software programs that come to mind that do this are Mathematica and Maple. Unfortunately both are prohibitively expensive for an individual. Thus mathematics is biased in favor of the rich. This is a new cultural development! In the past a pad and a pencil opened the doors to anyone so inclined. Now emath favors a small subset of the general population.
Me: There are a series of exercise on pages 8 - 10, but I have done some of these before and feel that I can proceed to the next section without difficulty.
Strang: 1.2 Lengths and Dot Products [p. 11 - 21]
The previous section described how to add (or subtract) any two (or more) vectors. This section is about multiplying vectors. There are many ways that one can imagine doing this. The trick is to come up with ways that are in some sense interesting and/or useful. One such way is called the dot product (also called the inner product).
Take two vectors with the same number of elements. Multiply each pair of numbers. Then add all of these products to create a single number. That number is called the dot product.
Me: Let's try this using APL.
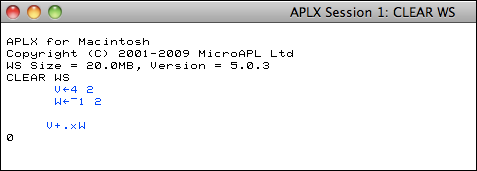
Note that I have created 2 vectors V and W and assigned 2 values to each vector. The notation in APL for computing the dot product is 3 symbols +.x . This is read from right to left: first multiply all of the corresponding elements, then add all of these intermediate products. The result in this case is zero. I really like the mnemonic value of the plus-dot-times symbol.
Strang: When the dot product is zero, this indicates that the two vectors are perpendicular (i.e. orthogonal) to each other. This is another way of saying that the two vectors are independent.
Now consider the dot product of a vector with itself.
The result turns out to be the square of the length of the vector. Think of Pythagorus' Theorem.
That is, the length of a vector is the square root of the dot product of a vector with itself.
The unit vector is the vector divided by its length.
The cosine of the angle between two vectors is the dot product divided by the product of the two lengths.
May 5, 6:20 am Mathematics
A search of the files on my computer using "Goodman" quickly identified a number of previous web pages that I had created in 2008. A check of a couple of these and I had the title of the book, "Algebra: Abstract and Concrete" by F. Goodman (2006). Success. Typing the title into google gave the website for the pdf file of the book. It is a free download (!) asking only that the user "make a generous donation to some organization devoted to relieving the misery of the world".
As an aside, I think this is the first time that I have used my website to find a previous reference.
I have even found the cardboard cutouts that I used to complete some of the early references.

Let me gather a few thoughts.
I now have 5 different resources at hand:
- Gilbert Strangs "Introduction to Linear Algebra" (2009), plus his MIT lectures on youtube
- Charles Pinter "A Book of Abstract Algebra" (1990)
- Avner Ash & Robert Gross (2006) Fearless Symmetry
- John Conway et al "The Symmetries of Things" (2008)
- Frederick Goodman (2011) "Algebra: Abstract and Concrete".
All 5 resources essentially cover similar topics, but with different emphases and examples. Let's try another conversation.

Me: Goodman's preface contains some important comments on the importance of thinking things through for yourself. He cautions that this is difficult and often frustrating and can't be learned quickly. It takes time. Which is what I have.
It has been 4 years since I last looked at the Goodman book, and I only made it through the first ten pages.
Goodman: "What is symmetry? Imagine some symmetric objects and some nonsymmetric objects. What makes a symmetric object symmetric? Are different symmetric objects symmetric in different ways?" [p. 1]
Me: These are good questions. It is easy enough to come up with a verbal answer but Goodman soon shows how a mathematician would answer this. A symmetry is a motion (i.e. transformation) that leave the object unchanged. For example, if one has a square and rotates it 90 degrees, then it still looks the same. An object is symmetric if it has symmetry motions.
This is the whole point of the Conway book! It then provides a notational system (first developed by Murray MacBeath) for describing these motions. This notation uses a star (*) and a point (.) where the star symbolizes the idea of series of mirror lines as in a kaleidoscope and the point symbolizes the idea that the symmetries fix a point. Thus *3. means 3 mirror lines of symmetry that fix a point in the center. An equilateral triangle has *3. symmetry. This quickly gets complicated but it serves a useful purpose when the patterns become complex.
I have now read the first three sections of chapter 1. They show the value of adopting some form of notation for representing different symmetries. The next section will show some connections between symmetry and matrix notation.
May 4, 8:40 am Mathematics
Chapter 2 Operations [p. 19 - 24]
I have completed exercises 2, 3 and 7 in part B (Properties of Operations). Exercise 7 had an answer at the back of the book which corresponded with mine. Good.
I looked at the exercises in parts C and D and have decided to move on to the next chapter on Groups.
The advantage of doing the exercises was primarily about developing skill in manipulating symbols. I need some practice with this so that was worthwhile. In general I am also aware that depending on the way an operation is defined, any combination of commutativity, associativity, and existence of identity elements and inverses is possible. Take nothing for granted when dealing with a new operation. A couple of non-algebraic operations are concatenation and permutations. Neat.
When I began this activity at 7:20 am I was still feeling somewhat lethargic, but focusing on the exercises soon had me feeling alert as I concentrated on the task at hand. This surprised me - I was prepared to give up early as I wasn't sure I was ready to do this at the time, but instead it became a way of waking up. I'm not sure if this will aways work. Then again, maybe it will.
May 3, 8:10 am Mathematics

I have begun actually "doing" some mathematics using "A Book of Abstract Algebra" by Charles Pinter (1990).
Chapter 2 Operations [p. 19 - 24]
I have completed all 6 exercises in part A (Examples of Operations) and the first exercise in part B (Properties of Operations). However I am not sure that I am doing part B properly. I want to reread this before continuing. I feel that I have a good grasp of the idea of an operation on a set of elements but am not sure that I am manipulating the symbols properly when working with the identity and inverse elements.
It was a pleasure to be using a fountain pen again.
I recall reading something a while ago that said that we are no longer teaching cursive writing in elementary school. I can see this as not being overly problematic when considering the move to keyboards and screens, but it seems to me that it will have major repercussions for mathematics and by extension to other areas that use mathematical notation such as science and statistics. Creating a mathematical expression using current software is cumbersome at best and it definitely interferes with the flow of thinking.

I want to adopt a two-fold approach to my learning by alternating my activities between two books. The second book is the 2006 book, "Fearless Symmetry" by Ash & Gross. This book is 15 years newer and has a more modern flavor. I started this book a few years ago and then let it go. I want to try again. I will begin with a dialogue between me and the book and then move to cursive notes when the symbolism suggests that is a good idea.
Chapter 1 Representations
Ash: " ...the basic concept of representation ... is the key concept underlying the number-theoretic methods of Galois representations" [p. 3]
Me: representation is very similar in nature to the idea of an operation (Pinter). But I have no idea of what a Galois representation is.
Ash: "Representations ... explain one thing by means of another. The object we want to understand is the 'thing': ... The object that we know quite a bit about already, to which we compare the source via a representation, we call the standard object." [p. 5]
Ash: They then provide a series of definitions.
- A set is a collection of things, which are called the elements of the set.
- A one-to-one correspondence from a set A to a set B is a rule that associates to each element in A exactly one element in B, in such a way that each element in B gets used exactly once, and for exactly one element in A.
- A function from a set A to a set B is a rule that assigns to each element in A an element of B.
- A morphism is a function from A to B that captures at least part of the essential nature of the set A in its image in B.
- A representation is a morphism from a source object to a standard target object.
"When A and B have some additional 'structure' (e.g. they are finite sets, or ordered sets) and we restrict the possible morphisms from A to B to have something to do with that structure ... then the existence of a representation from A to B gives us some information about A in terms of the standard object B (e.g. how many elements are there in A)
Me: The setting up of these definition may seem a little pedantic, but it leads to clarity of thought within this restricted domain. The ideas of this chapter are almost identical to the ideas of an operation that Pinter describes. Slightly different terminology, and perhaps nuances of interpretation, but very, very similar. So far, so good. Each book reinforces the other.