
Home
Journals 2008
Year to Date
January
February
March
April
May
June
July
August
September
October
November
December
Time Tables 2008
Year to Date
January
February
March
April
May
June
July
August
September
October
November
December

Year to Date
January
February
March
April
May
June
July
August
September
October
November
December
Year to Date
January
February
March
April
May
June
July
August
September
October
November
December
This page last updated on: Friday, May 9, 2008 4:18 AM
It is +2 C with a high forecast of +11 C. Sunrise 5:56 Sunset 20:59 Hours of daylight: 15:03
The weather remains cool and wet. A good day for a cup of hot coffee and a little mathematics.
| Learning Category | Planned Activities for Today | Time |
|---|---|---|
| Literature | Begin morning with a Rumi reading | |
| Literature | Continue reading "The Interpretation of Murder" by Jed Rubenfeld | 1 hr |
| Mathematics | Make notes on symmetry - 10 | 2 hr |
Here is my chart of symmetry readings: Each cell will corresponds to a chapter. Yellow indicates the number of chapters in the book, green indicates that I have read and made notes on the chapter. The background colors of the book titles are purple for mathematics books where one actually does the mathematics and light blue indicated books that describe what others have done. In an ideal world on each day I should be able to add at least one cell to what I have read.
|
A quick review of my notes for yesterday shows that I have begun studying symmetry and groups from a geometric perspective. The third chapter of Fearless Symmetry begins a description of permutations. Looking at Groups and Symmetry", permutations is the topic for chapter 6. "Groups: A Path to Geometry" begins with functions and then treats permutations in chapter 2. I think it makes good sense to look at chapter 1 of "Groups: A Path to Geometry" first.
This is a fascinating book. The text for chapter 1 is less than a page. This is followed by 6 pages of problems. The notational conventions make it necessary to use a hand-written approach for this activity. These notes will then be scanned and inserted below. I am looking forward to using my Pelican fountain pen, and my Rhodia pad of paper, for this. I prefer using Dreamweaver CS3 for making notes, but definitely prefer pen and paper for "doing" mathematics.



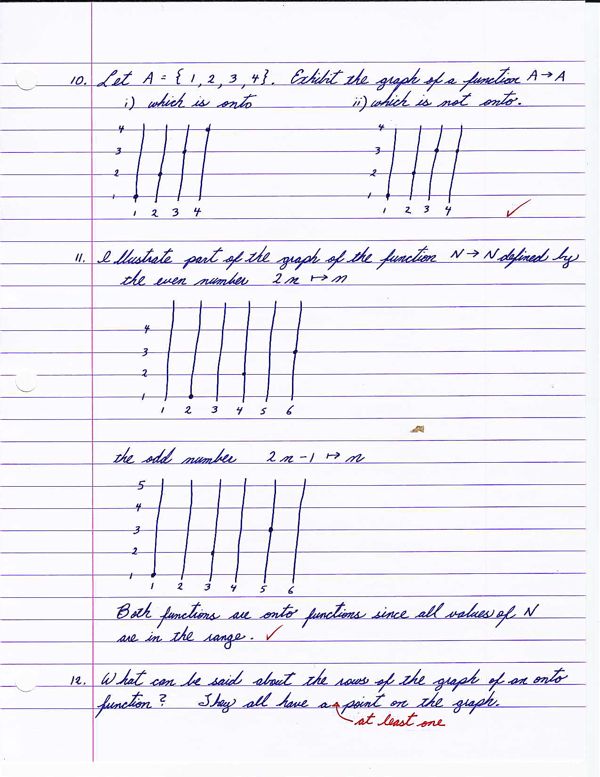
I am now familiar with the graph notation for discrete functions as well as the difference between an onto function and a not onto function. I need to focus more carefully on being very precise in my wording of some statements. I still have a tendency to make silly (careless) mistakes - such as when I wrote 4 x 4 when I had already argued that it should be 4 raised to the power of 4.
I have now completed the first 12 questions for chapter 1. There are a total of 34 questions, so I am just over a third of the way through the chapter. I am going to have to use my jusgement on which questions should be answered explicitly and which can be skimmed over with a comment like "I can do this." The issue is one of finding the balance between learning & practice and being pedantic and redundant. The approach Burn takes is very close to that taken by the Schaum's Outline series, the difference being that with Burn the answers are collected at the end of the chapter, whereas Schaum's provides the answer immediately after each question. Both types of book emphasize the "doing" aspect over a strong didactic approach. But my approach is to add a summary section after each chapter (or after each session) that describes the ideas and procedures that I have learned in that chapter. |
Tags: mathematics, function, morphism, representation, group
We have moved the bedding plants into the garage. The overnight low is forecast to be +1 C but snow is also forecast. We shall see.
Books on the Go Today |
|
 |
 |
 |
 |
 |
 |