Wednesday May 7, 2008 8:00 am Lethbridge Alberta

Date Mathematics History 500 BCE Pythagorus   399 BCE Thaetetus classifies the 5 regular Platonic solids in 3 dimensions: tetrahedron, cube, octahedron, dodecahedron, icosahedron.   1048 - 1131 Omar Khayyam finds geometric method for solving cubic equations.   1200 Leonardo Fibonacci wtote the first original book on mathematics published in Europe. It introduced Hindu-Arabic numerals and place-value notation.   1439   Gutenberg invents the printing press 1452 - 1519   Leonardo da Vinci 1492   Columbus discovers America early 1500s del Ferro, Tartaglia, Cardano, Ferrari solve cubic & quartic equations   1564 - 1642 Galileo   1642 - 1727 Isaac Newton   1775 - 1783   American War of Independence 1777 - 1855 Carl Friedrich Gauss   1789 - 1799   French Revolution 1802 - 1829 Niels Henrik Abel proves that no formula exists for equations of degree 5.   1832 Evariste Galois dies at age 20.   1842 - 1899 Sophus Lie: Norwegian group theorist       Here is my chart of symmetry readings: Each cell will corresponds to a chapter. Yellow indicates the number of chapters in the book, green indicates that I have read and made notes on the chapter. The background colors of the book titles are purple for mathematics books where one actually does the mathematics and light blue indicated books that describe what others have done. In an ideal world on each day I should be able to add at least one cell to what I have read.   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23                             Symmetry                                                                           Fearless Symmetry                                                                           Algebra                                                                           Abstract Algebra                                                                           Creating Escher-type Drawings                                                                           Handbook of Regular Patterns                                                                           Symmetry & the Monster                                                                           The Celtic Design Book                                                                           Groups & Symmetry                                                                           Groups: A Path to Geometry

I want to try a slightly different approach to this set of notes. The idea is to provide a story that describes my efforts at Learning about symmetry and group theory.

The above table indicates the resources that I have at my disposal. Some of the books describe what mathematicians have learned about this topic but do not give a sense of the actual mathematics that are involved. The books with a purple background are more like textbooks that attempt to have the reader develop skills for future use. That is my goal.

Because of the difficulties of incorporating the various notational conventions onto this web site, my efforts will consist of a blend of web-based activities and hand-written notes (which will be scanned and inserted in these web pages).

Fearless Symmetry. Chap. 1 Representations

I have scanned the first chapter of each of the five "purple" books and have decided to begin with the first chapter of Fearless Symmetry.

This begins with a number of basic definitions and ideas that will be used on on almost daily basis. What are these basic ideas?

• representation
• set
• one-to-one correspondence
• function
• morphism

I keep reminding myself that these notes are not the important product. The important product is my mental understanding of these terms, how they are related, and how they may be utilized to answer certain types of questions and to generate new ideas. Thus these notes my be viewed as a representation of my mental structure.

Definition: A representation is a morphism from a source object to a standard target object.

Usually, within mathematics, the standard target object is some form of mathematical structure that we already know quite a bit about. The motivation behind forming a representation is that we may then use this knowledge of the target object to infer some additional properties of the source object.

I want to try to create a few more details of this standard target object (i.e. these notes) and then see if that helps me understand the five ideas mention above.

Here is my first attempt at using a software package called Cmap to create a concept map for the five ideas in this chapter:

Summary

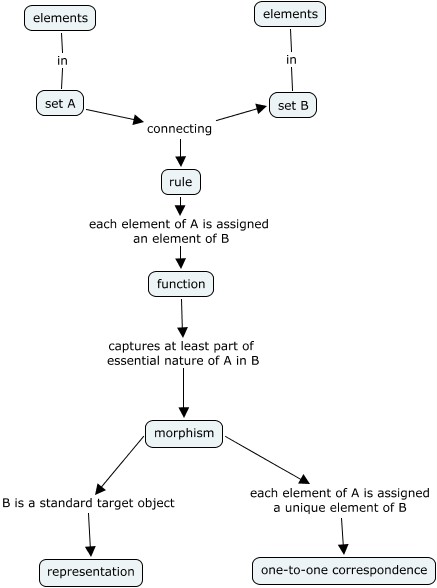
A morphism is a special type of function that captures some essential feature of A in its image in B and a representation is a special type of morphism that uses a standard target object for B. Then since we know quite a bit about B, this allows us to make some additional comments about the nature of A. I have also learned two new ideas and their associated names: morphism and representation.

There is nothing difficult with the ideas presented in this chapter. I am delighted with this type of beginning where I can focus on understanding the nature of the key terms and concepts at the outset and then burrow in to learn some techniques that involve these ideas. I also like the idea of having a synopsis of each chapter at the beginning. This gives me an initial framework for appreciating what I am reading. I also like the idea of a summary of the key points at the end of the chapter. It does take a while to become familiar with a new software package. I am not yet convinced that the cognitive map is worthwhile (at least in its present form).

Fearless Symmetry. Chap. 2 Groups

• "Mathematical sets can be interesting and easy to define, but very hard to understand in detail. ... If a set can be endowed with extra structure, it can help our understanding. One very common kind of extra structure is a 'composition law' that turns the set into a group." [p. 13]

Keep in mind that a set is simply a collection of elements. A group is a set with additional properties.

• "The definition of a group is the most common way mathematicians have of formalizing the concept of symmetry." [p. 13]
  
  
• "There is a lot known about groups in general and about special kinds of groups in particular, and we will be able to deplay all this knowledge when we can impose a group structure on the objects we want to learn about." [p. 13]
  
  
• "... we will look at a particular example, the group SO(3) of the rotations of a sphere. SO(3) stand for 'special orthogonal group in three dimensions' " [p. 13]

The label SO(3) seems a bit cumbersome. But it does introduce me to the type of labels I might expect in the future.

• "A group is a set along with a rule that tells how to combine any two elements in the set to get another element in the set." [p. 14]

Definition: A Group G is a set with a composition defined on pairs of elements , as long as three axioms hold true:

1. There is a neutral element e in G, so that x o e = e o x = x
no matter what element of the group is substituted for x.

2. For any element x of G, there is some element y in G so that x o y = y o x = e . ( y is called the inverse of x ).

3. For any three elements x, y, and z in G, we have (x o y) o z = x o (y o z). (This is called the associative law).

Definition: If G is a group, the group law is the rule that tells how to combine two elements in the group to get the third.

• "Since SO(3) consists of the rotations of a sphere, there is also the idea of an infinitesimal element. ... Any actual rotation should be buildable by integrating some infinitesimal rotation. This is the germ of the theory of Lie groups and Lie algebras." [p. 19]
  
  
• "A group such as SO(3) that has infinitesimal generators is called a continuous group. The other main type of group is called a discrete group." [p. 19]

This is another simple chapter. One new idea is described - the general concept of a group, and its mathematical definition is given. Two main types of group are mentioned: continuous (Lie) and discrete.

Tags: mathematics, function, morphism, representation, group