
Journals 2007
Notes
Literature
Mathematics
Technology
Birding
ModelTrains
Philosophy
Psychology
Science
History
Time

Journals 2007
Notes
Literature
Mathematics
Technology
Birding
ModelTrains
Philosophy
Psychology
Science
History
Time
It is +7 C with a high forecast of +24 C. Sunrise 6:12 Sunset 21:01 Hours of daylight: 14:49
The first step this morning will be coffee. Maybe that will help me think of a next step.
I am pleased with a purchase that I made a couple of days ago. I bought two reading glasses at only $2. a piece. Then I threw away the glasses and kept the cases. They make a perfect carrying case for my Pelikan pen. This even plans for the future in the event I ever decide to buy a second pen. At the moment the Pelikan rests in a small glass vase that I bought in a shop for $3. Here is a still life photo that I took a few minutes ago. Since this is still early morning, the coffee is an essential prop.

| Immediate | Description | Time |
|---|---|---|
| Literature | Continue reading "Number 9 Dream" by | 1 hr |
| Mathematics | Make notes for week 1b of "The Humongous Book of Calculus Problems" | 1 hr |
| Mathematics | Complete problems 5.9 - 5.12 of "The Humongous Book of Calculus Problems" | 1 hr |
| Mathematics | Continue reading "The Black Swan" by Nassim Taleb | 1 hr |

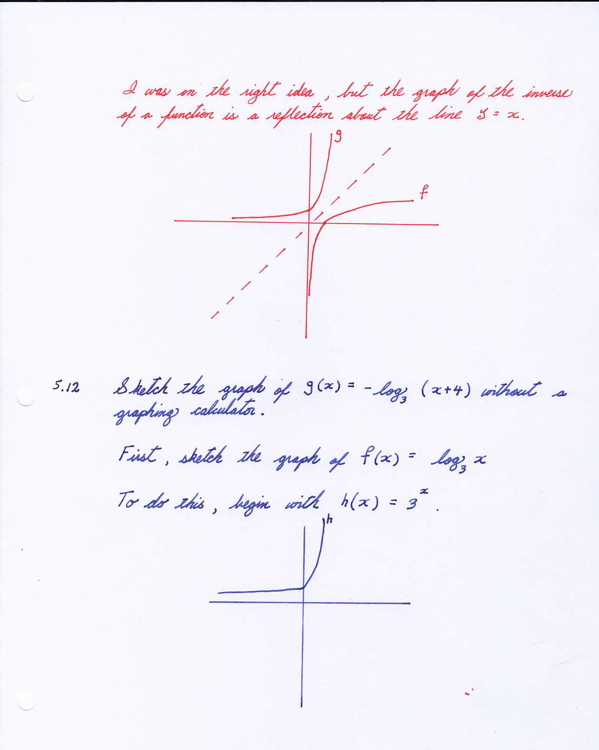
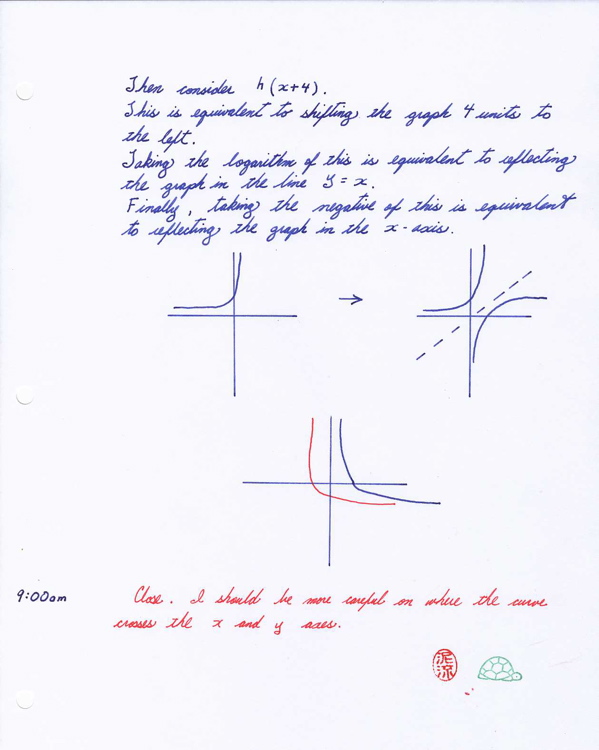
I am still having some difficulties with this, but really am enjoying the idea of sketching a graph by transforming a simpler graph. This is new to me, but it is a nice way of thinking about the graph.
Now to try setting up the framework for section 1.2 Linear Inequalities and Interval Notation
Session 2 (Week 1b)
Chapter 1 Linear Equations and Inequalities
Section 1.2 Linear Inequalities and Interval Notation
1. Activities
W. Michael Kelley (2006). The Humongous Book of Calculus Problems.
Complete problems 1.11 - 1.20 [p. 5 - 8]
Wayne W. Dyer (2007). Change Your Thoughts - Change Your Life.
Read Verse 2: Living the Paradoxical Mystery [p. 7 - 12]
2. What's it all about?
This section extends the idea of equality to inequalities and describes how to graph an inequality on the number line as well as how to write an inequality using a notational convention involving parentheses and brackets.
3. What am I able to do, now that I am finished this section?
Given an inequality equation, I can represent it on a number line and I can represent it symbolically.
4. What will I know?
I understand the basic idea of an inequality and that it can be represented both graphically and symbolically.
5. What are the key concepts?
6. What are some relevant Web sites for this material?
Using your favorite search engine, and maybe one or two others, type in a few key words such as "linear inequality" or "graphing linear inequality" or "solving linear inequality" .
Here are four Web sites that I liked:
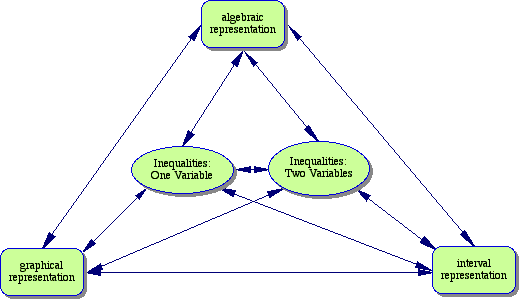
7. What concept map can I create for this section?
8. What types of Mathematica activities can I create?
Mathematica can produce plots for a set of inequalities that are far more complex than one would normally try to envisage by manual means. Even if one does not have Mathematica, seeing a few examples of such plots can expand one's imagination of what is possible.
Here is a Mathematica Notebook for this section.
9. What are some connections to other ideas?
The idea of an inequality is simply an extension of the idea of an equation. Instead of finding a value of an unknown variable that satisfies an equation, one tries to find all of the values of a variable that are less than a particular equation.
10. What is my overall reaction to this section?
This is a very short and simple section. There are only a couple of new ideas, and they involve notation more than some type of complex manipulation of symbols.
11. Comments on Dyer: 2. Living the Paradoxical Mystery
This section discusses the idea of thinking of dichotomies such as beauty - ugly as a continuum and that everything has a varying amount of both. In the case of mathematics one such continuum might be easy - hard. But nothing is easy, or hard. Rather an item or situation has varying degrees of both, depending in large upon the previous background of the individual. Even the idea of a single dimension is restrictive, both in reality as well as in mathematics. Everything is highly multidimensional. Within mathematics this should be an automatic extension of most topics. If this is an idea in 2-dimensions, can it be extended to 3-dimensions? Or 4, or more generally, to n-dimensions, where n is a positive integer? What about fractional dimensions? Is there a way that it makes sense to consider this? (The answer to the last question is, surprisingly, sometimes yes. This is a topic within the general area of fractal geometry and non-linear dynamics, also referred to as chaos theory.)
I am now spending a little leisure time playing with the crossword puzzles in "The New York Times Easy Crossword Puzzle Omnibus" which contains 200 puzzles. So far, I have begun 20 puzzles and have completed 12.
This chapter is one that will be very important for me in the future. I need to strengthen my deep understanding of logarithms and how to manipulate them.