
Journals 2007
Notes
Literature
Mathematics
Technology
Birding
ModelTrains
Philosophy
Psychology
Science
History
Time

Journals 2007
Notes
Literature
Mathematics
Technology
Birding
ModelTrains
Philosophy
Psychology
Science
History
Time
It is +15 C with a high forecast of +26 C. Sunrise 6:11 Sunset 21:03 Hours of daylight: 14:52
I am up early this morning.
| Immediate | Description | Time |
|---|---|---|
| Literature | Continue reading "Number 9 Dream" by | 1 hr |
| Mathematics | Continue ch. 1 of "A Transition to Advanced Mathematics" | 1 hr |
| Mathematics | Complete problems 5.1 - 5.8 of "The Humongous Book of Calculus Problems" | 1 hr |
| Mathematics | Continue reading "The Black Swan" by Nassim Taleb | 1 hr |
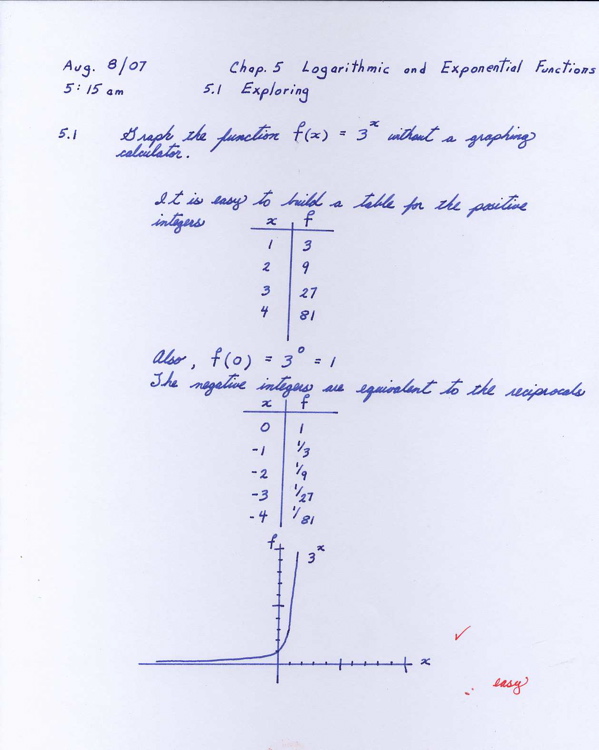
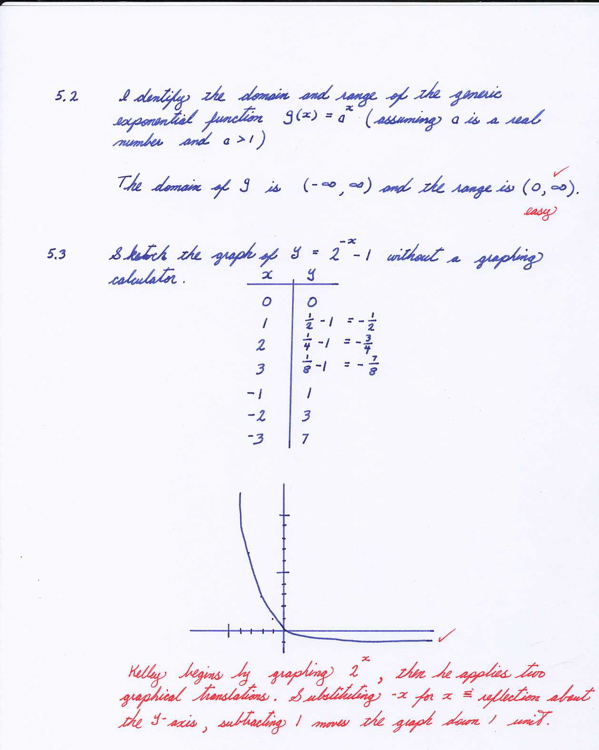


I am benefitting from these exercises. I definitely need more practice, particularly with expressions involving logarithms. These exercises also ensure that I am familiar with the various operations involving positive and negative fractional exponents.
There is something subtle going on here with this notation. When an exponent is a whole number, the idea is simple - one multiplies the number by itself a certain number of times. But what does it mean to mutiply a number by itself 2/3 of the time?
I want to continue to work on the overall description of the activities that I began on August 6.
Preface
The original idea was very simple: I wanted to relearn some of the mathematics that I studied about 40 years ago, but which I had forgotten, largely because I did not use it. Two topics were of particular interest to me: calculus and abstract algebra.
These notes were developed as I began my self-initiated program to learn calculus. After reviewing a number of calculus textbooks and resources I finally decided to focus on one in particular, Michael Kelley's "The Humongous Book of Calculus Problems". The book had a few attractive features. I was impressed that he devotes eight chapters to preparatory activities before beginning with the key idea underlying calculus: limits. I definitely felt that I could benefit from such an extensive review of the prerequisite ideas and problem solving exercises. Much of this material is at a high school level, but it is necessary to be sure of one's pre-requisites before proceeding.
After I had completed the first four chapters of Kelley's book, I happened to buy a book on a totally unrelated topic, the application of Taoist thinking and philosophy to one's daily life. This was a book by Wayne Dyer called "Change Your Thoughs - Change Your Life". Almost immediately I could see strong connections between this book and what I was trying to accomplish with calculus. In addition, I liked the overall structure of Dyer's book and decided to see what would happen if I tried a similar approach.
Thus the overall strategy for this personal learning experience is to complete set aside time over a three-day period to cover one complete section from Kelley's book. Since there are a total of 114 sections, this adds up to 342 days. In addition, I plan to read one section of Dyer's book during the same three-day period. Dyer has 81 sections, so I will finish his book slightly ahead of the Kelley book, but that is not a problem. After completing the exercises and reflecting on Dyer's commentary, I will spend an hour or two summarizing what I think I have learned by creating in my own notes under 11 sub-headings.
I also would like to utilize some of the latest computer software to supplement the two books and my own handwritten efforts at completing the exerises described by Kelley. I hope to use a package called Mathematica to further explore some of the ideas that arise while working through the problems in Kelley's book (there are 1,000 of them), but any good graphing utility should be satisfactory. Second, I plan to use a concept mapping software program called Inspiration to create diagrams that illustrate the relationships among the various concepts as I encounter them. Once again, there are a number of such programs on the market and any one of them would be fine. Finally, I definitely will be using the Web and a few search engines to locate additional information as questions and difficulties arise.
I have a good laptop (MacBook Pro), a high-speed internet connection (ADSL), as well as two software packages (Mathematica and Inspiration) so I am set from a high-tech perspective. I am also well equipped from a low-tech viewpoint: I just purchased a new fountain pen (a Pelikan M250 Traditional), a good bottle of ink (Waterman's Florida Blue), and some excellent blank paper (Xerox Premium Multipurpose, 24 lb, 96 brightness).
Let the good times roll!
Session 1 (Week 1a)
Chapter 1 Linear Equations and Inequalities
Section 1.1 Linear Geometry
1. Activities
W. Michael Kelley (2006). The Humongous Book of Calculus Problems.
Complete problems 1.1 - 1.10 [p. 1 - 5]
Wayne W. Dyer (2007). Change Your Thoughts - Change Your Life.
Read Preface and Verse 1: Living the Mystery [p. xi - xvi, 1 - 6]
2. What's it all about?
Kelley begins with a series of problems involving points and straight lines. These are discussed both algebraically and graphically. Graphically, a straight line, and a point, are two of the simplest graphical objects. Algebraically, the equation of a straight line, and the idea of the (x,y) coordinates of a point, are two of the simplest algebraic expressions. It makes sense to be comfortable with these ideas before looking at more complex situations.
3. What am I able to do, now that I am finished this section?
I should be able to solve most problems involving the algebraic formulation of lines and points.
4. What will I know?
I will know the key terms and definitions and be able to apply them in the solution of problems involving such terms.
5. What are the key concepts?
6. What are some relevant Web sites for this material?
Using your favorite search engine, and maybe one or two others, type in a few key words such as "linear equation" or "analytic geometry" or "mathematics inequality" or "Rene Descartes".
If you see a Web page that is clearly beyond your understanding, simply continue browsing until you find a few that are at about your level. Sometimes it is fascinating to skim a page and see if you can even get a sense of what is being discussed. If nothing else, you at least realize that there is more here than you suspected.

8. What types of Mathematica activities can I create?
One possibility is to create a graphical environment with 3 lines, each a different color. Then one can move these line around by changing the formula and see what interesting questions emerge. One of the difficulties is becoming familiar with the notational conventions of Mathematica. But this has a positive aspect as well - it provides an alternative system so one can realize the arbitrariness of each. It also provides a context within which one can compare the strengths and weaknesses of each. Notational systems are not right or wrong, but strong or weak for a given situation.
Here is a Mathematica Notebook for this section.
9. What are some connections to other ideas?
There are two obvious prerequisites to even this discussion of points and lines. One is the idea of number. Another is the idea of the x-y coordinate plane.
A brief comment on number. There is much about numbers that even mathematicians do not understand. Even the simplest types of number quickly lead to questions that have puzzled people for generations. The simplest type of number is a positive integer. These are the familiar counting numbers: 1, 2, 3, ... . If one includes zero and all of the negative integers, then one has all of the integers. There is an entire branch of mathematics that discusses arithmetic with such numbers. It turns out that the hot topic of cryptography where one tries to create a code that cannot be broken is hevily dependent on the properties of such integers. There are other types of numbers that even young children are familiar with: fractions. These are often a source of confusion but everyone is at least familiar with a few of the basic facts about such numbers. Most people know that one-half is larger than one-third, although far fewer know how to do arithmetic involving fractions with confidence. There are other types of number as well, but this gives you a sense that there is more here than one realizes at first glance.
Another brief comment on the x-y coordinate plane. This idea, due to a French philosopher and mathematician, Rene Descartes (1596 - 1650), is one of the most powerful ideas in all of mathematics, yet we quickly take it for granted. The idea is that the position of a point on a flat surface can be identified by two numbers, one of which specifies the distance from an arbitrary line called the x-axis and the other of which specifies the distance from another line called the y-axis. From this simple idea the entire field of analytic geometry is developed. The power of the idea lies in the fact that now one can move between two totally different ways of representing an idea. The idea of a straight line is intuitively thought of as a graphic image. But it may also be thought of as a set of points satisfying a particular algebraic equation. It turns out that it is usually much easier to manipulate such equations and discover new patterns and relationships than it is to work with the graphic images which are usually drawn somewhat imprecisely.
Thus, although we begin with apparently simple ideas such as point and line, they are both built on a foundation that is itself fascinating. And both the idea of number and the idea of a flat surface can be extended to include a variety of other kinds of number and other kinds of surfaces.
10. What is my overall reaction to this section?
There is much more here than I realized!
11. Notes from Dyer: 1. Living the Mystery
One of the great mysteries of science is that our man-made mathematical ideas and logical relationships provide such a good way of describing the indescribable natural world. After all, that is what our equations provide: a way of describing physical reality and increasingly, social reality. Amazing. Really amazing. Why should it be so?
This is becoming a fairly good framework for each sub-section. Now to see how well it works for the next few sections.
I want to begin the exercises for chapter 5 of "The Humongous Book of Calculus Problems" which is called Logarithmic and Exponential Functions. Up until now I have been playing with polynomial functions. The collection of polynomial, exponential, logarithmic and trigonometric functions together with all possible finite combinations and compositions are usually referred to as the elementary functions. These are the basic functions that one uses when beginning a study of calculus.
I now seem to have a fairly good understanding of algebraic polynomials but both exponential/logarithmic and trigonometric functions could use a little review.