
Journals 2007
Notes
Literature
Mathematics
Technology
Birding
ModelTrains
Philosophy
Psychology
Science
History
Time

Journals 2007
Notes
Literature
Mathematics
Technology
Birding
ModelTrains
Philosophy
Psychology
Science
History
Time
It is +14 C with a high forecast of +29 C. Sunrise 6:09 Sunset 21:05 Hours of daylight: 14:56
Another early morning. Great. I have a coffee scheduled for The Ugly Mug at 8 this morning. My early coffee is on the boil. I'll set up the web pages and then do a little math. I think I have pen, ink and paper now under control.
| Immediate | Description | Time |
|---|---|---|
| Literature | Begin reading "Number 9 Dream" by | 2 hr |
| Mathematics | Continue ch. 1 of "A Transition to Advanced Mathematics" | 1 hr |
| Mathematics | Complete problems 4.29 - 4.34 of "The Humongous Book of Calculus Problems" | 1 hr |
| Mathematics | Continue reading "The Black Swan" by Nassim Taleb | 1 hr |
The idea of copy-and-pasting entries from this web site into a Word file (with little formatting and no images or notes or time management tables) seems to be a good way of seeing the month at a glance. If I also print out the monthly chronology page as well, I have a fairly good snapshot of the month's Learning activities.
I am not sure how I want to approach the various notebook files that I have created. In the back of my mind, I realize that this idea lends itself to an XHTML/CSS approach where I simply use a different style sheet for the printer.
I am also mulling over a number of ideas about mathematics learning and notemaking. Much to my surprise, a lot of this has come from reading the first few pages of the book I bought yesterday on the Tao. I even have a title: The Tao of Calculus: A Personal Way of Learning. Basically the idea is to emphasize relaxing and letting the math lead you along the path. This then leads to a more playful attitude toward the topic and to encouraging one to ask questions. I am actually quite excited about this as a framework for discussing how to approach the learning of any topic.
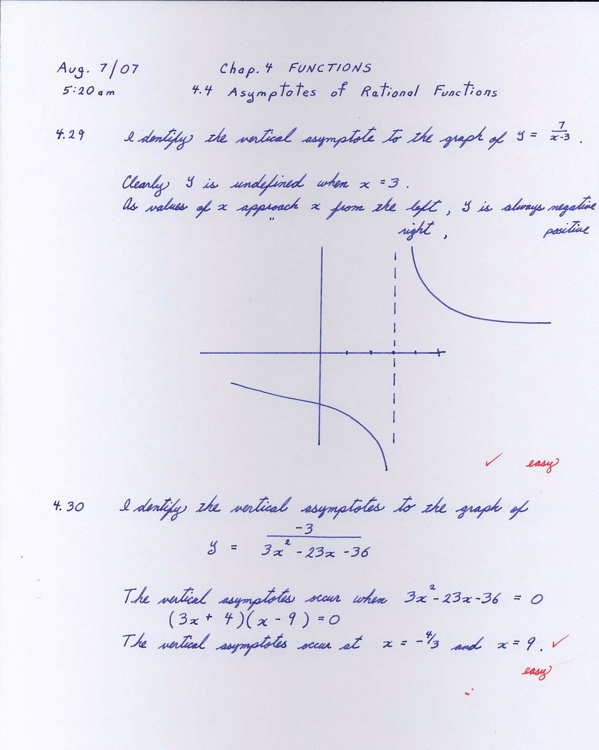


This was a definite shock. I was not able to follow the argument in Kelley, so I tried Google with "slope intercept algebra" and then again, adding the term hyperbola. I now realize that the topic of slant asymptotes is embedded within a discussion of the graphs of hyperbolas. This is a topic that I think I once covered in high school, but doubt that I ever used again. Here are a couple of web sites that discuss this:
http://tutorial.math.lamar.edu/classes/alg/hyperbolas.aspx
http://fhh.fhsd.k12.mo.us/rrenken/PowerPoints%20&%20Notes/Algebra%202/Chapter%207/Alg2%20Section%207-5%20Hyperbolas%20part%201.pps (this is a powerpoint file)
http://www.tpub.com/math2/18.htm
Looking at these sites, I realize that a better search term would be "conic sections".
http://www.krellinst.org/UCES/archive/resources/conics/
http://xahlee.org/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html
http://en.wikipedia.org/wiki/Conic_section
I then had a look at the table of contents for Kelley's "The Humongous Book of Calculus Problems" and see that the topic of conic sections is covered in detail in chapter 6. I will wait until I look at this before focusing on this topic.
I thought about this while walking to and from coffee. Kelley mentions that one has a slant intercept when the highest power of the variable in the numerator is one more than the power of that variable in the denominator. But when I was on the web I only saw examples of hyperbolic functions where the numerator is a quadratic and the denominator is less than that. This quickly gave rise to two reactions:
1. I could use Mathematica to obtain some curves and see what they look like aka Kelley.
2. I could use Mathematica to see what happens to the shape of the curves as I play with the various parameters. This later is important as it will give me a sense of the effect of different values on the curve. The issue of the equation of the asymptote is more a matter of algebraic manipulation. This will give me the answer, but I still have little idea of what is actually happening.
The first step is to review the steps for obtaining a graph using Mathematica. This may also involve learning about something called a parametric plot.
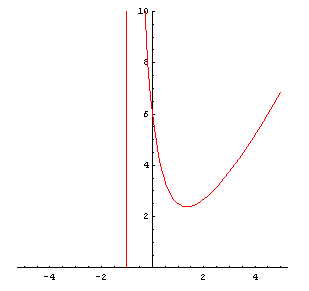
Here is a sample graph for the equation in exercise #4.34 . This is a beginning. One can see that there is likely a slant intercept along the right hand side of the curve, but the curve does not include values of y that are negative.
Here is the graph with both parts showing:
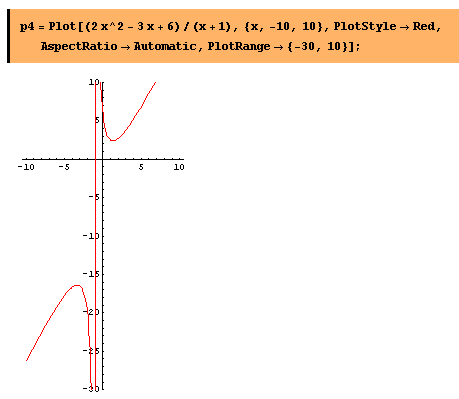
At the moment this entire process of using Mathematica in Parallels and then copying and saving the image in a Dreamweaver folder is very cumbersome. Also I do not know how to draw the slant asymptote on this graph.
It is more than a little frustrating to figure out how Mathematica graphs functions.
Three more books arrived today:
That takes care of all the books that were on order.
I now have two calculus threads on the go. One is the problems for chapter 4 on Functions. The other is a catch-up activity as I play with some additional notes for my activities. But I want to begin the day by doing a few more problems, using my fountain pen.