Chapter |
Terminology (concepts) |
Description |
Notation |
| Part One |
Algebraic Preliminaries |
|
|
1 |
Representations |
|
|
|
set |
A set is a collection of things, often called the elements of the set. |
{a, b, c} |
|
one-to-one correspondence |
A one-to-one correspondence from a set A to set B is a rule that associates to each element in A exactly one element in B, in such a way that each element in B gets used exactly once, and for exactly one element in A. |
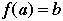
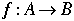
|
|
standard object |
This is an object that we know quite a bit about. |
|
|
function |
A function from a set A to a set B is a rule that assigns to each element in A an element of B. |
|
|
morphism |
A morphism is a function from A to B that captures at least part of the essential nature of the set A in its image in B. |
|
|
representation |
A representation is a morphism (i.e. a function) from a source object to a standard target object.
If A represents B, we have three things: two objects, A and B, which in this context will be sets, and the relation between them, which will be a morphism. When A and B have some additional "structure" (e.g. they are finite sets, or ordered sets, or ...) and we restrict the possible morphisms from A to B to have something to do with that structure. |
|
| |
Example:
Let A be the set {red, blue, yellow, pink}.
Let B be the standard object {1, 2, 3, 4}. Let f be the following rule: red is associated with 1, blue is associated with 2, yellow is associated with 3 and pink is associated with 4. f is a morphism because because this rule is capturing something about the number of elements in A. Therefore we may consider f to be a representation of A. |
2 |
Groups |
|
|
|
group |
A group G is a set with a composition defined on pairs of elements such that :
1. There is a neutral element e in G, so that 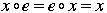 no matter what element in the group is substituted for x. e is sometimes called the identity element. no matter what element in the group is substituted for x. e is sometimes called the identity element.
2. For any element x of G, there is some element y in G so that 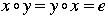 . That is, every element has an inverse element. . That is, every element has an inverse element.
3. For any three elements, x, y, and z in G, we have 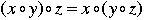 . This is called the associativity of the composition. Each group has its own law of composition. It can be whatever we define it to be (e.g. addition, multiplication, rotation, ...). . This is called the associativity of the composition. Each group has its own law of composition. It can be whatever we define it to be (e.g. addition, multiplication, rotation, ...). |
|
| |
group law |
If G is a group, the group law is the rule that tells how to combine two elements in the group to get the third. |
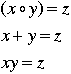 |
| |
discrete groups |
There is no smooth path from one element to another. (e.g. the integers under addition, permutation groups) |
|
| |
continuous groups |
There are infinitismal differences between elements. |
|
| |
Lie groups |
Pronounced "Lee", named after the Norwegian mathematician Sophus Lie who studied them. (e.g. rigid motions in space, rotations of a circle, rotations of a sphere, set of real numbers under addition) |
|
| |
Examples:
Consider the set Z of all the integers (positive, negative and zero). Z is an infinite set. Let the group law be familiar addition. Then Z under this group law is a group.
Consider the set of three rotations of 60, 120 and 180 degrees of an equilateral triangle. The rotations constitute the group law. The elements of the group are the three positions (i.e. orientations) of the triangle.
Groups are used to describe various types of symmetries. |
3 |
Permutations |
|
|
| |
permutation |
A permutation is a reordering of a set of elements. It is a function that assigns to each element of the set another element of the set such that it is a one-to-one correspondence. The function gives the rule for assigning each element. |
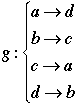 |
| |
group of permutations |
The collection of all possible permutation functions for a given set A forms a group. Notice that if A has n elements then  has n! elements. That is, there are n! different reorderings of n elements. has n! elements. That is, there are n! different reorderings of n elements. |
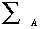 |
| |
identity permutation |
This is the function that leaves every element in the same position. |
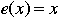 |
| |
inverse permutation |
This is the function that returns every element to its previous position. |
Let 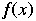 be a permutation of a set A. Then the inverse be a permutation of a set A. Then the inverse 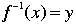 if and only if if and only if 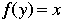 . . |
| |
cycle decomposition |
A particular permutation can be expressed as a series of cycles. For example, one such permutation of A = {a, b, c, d, e} may be a -> d -> a and b_> c -> e -> f-> c. |
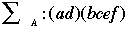 |
4 |
Modular Arithmetic |
Modular arithmetic is of fundamental importance in all of number theory. |
|
| |
conguence |
Congruence is a binary relation between two numbers similar to equality. Two numbers are said to be congruent modulo n if they have the same remainder when divided by n. |
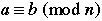 |
| |
modulus |
The number n that is the divisor is called the modulus of the congruence. |
|
| |
integer |
An integer is a whole number - positive, negative or zero |
|
| |
prime number |
A prime number is a positive integer greater than 1 that has no positive divisors except itself and 1. A negative number is also called prime if its absolute value is prime. |
|
| |
field |
A field is a number system where we can divide by anything nonzero. The integers modulo p (where p is a prime) are a field under addition and multiplication. We say that 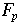 is a finite field with p elements. We also say that is a finite field with p elements. We also say that 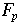 is a number system with characteristic p. Note that is a number system with characteristic p. Note that 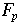 does not contain fractions. does not contain fractions.
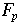 is a group under addition. is a group under addition.
If we delete the number 0 from 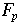 , we have a new set of p - 1 elements that is a group under multiplication. The new set is symbolized as "eff-pea-cross" : , we have a new set of p - 1 elements that is a group under multiplication. The new set is symbolized as "eff-pea-cross" : 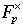 . . |
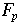
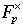
|
5 |
Complex Numbers |
|
|
| |
real number |
Any number that can be expressed as a decimal, either terminating or repeating. |
R |
| |
complex number |
A number of the form a + bi where a and b are real numbers. |
a + bi |
| |
complex conjugate |
A number of the form a - bi where a and b are real numbers. |
a - bi |
| |
set of all complex numbers |
|
C |
| |
Theorem |
Let 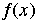 be a polynomial whose coefficients are any complex numbers. Then the equation be a polynomial whose coefficients are any complex numbers. Then the equation 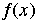 = 0 has solutions in C. = 0 has solutions in C. |
|
| |
algebraic closure |
The field C is closed under algebraic (i.e. addition, subtraction, multiplication, division, and the taking of roots) operations. This is a restatement of the previous theorem. |
|
| |
|
|
|
6 |
Equations and Varieties |
One of the main problems in number theory is finding and understanding all solutions of Z-equations. |
|
| |
rational number |
Any number that can be expressed at the ratio of two integers. |
|
| |
irrational number |
Any number that is not rational. |
|
| |
set of all rational numbers |
|
Q |
| |
Z-equation |
Also called a Diophantine equation. |
|
| |
set of all integers |
|
Z |
| |
set of integers modulo p |
|
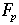 |
| |
variety |
The variety S defined by a Z-equation (or a system of Z-equations) is the function that assigns to any number system A the set of solutions S(A) of the equation.
Many different systems of equations can define the same variety S. |
S(A) |
| |
Fermat's Last Theorem |
For any positive integer n, let the variety 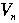 be defined by be defined by 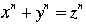 . Then if n > 2, . Then if n > 2, 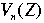 contains only solutions where one or more of the variables is 0. contains only solutions where one or more of the variables is 0.
It is easier to study 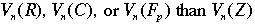 . Then some information about . Then some information about 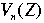 (the solution set we are really interested in) can be derived from the preceding three sets using advanced theorems from number theory and algebraic geometry. (the solution set we are really interested in) can be derived from the preceding three sets using advanced theorems from number theory and algebraic geometry. |
|
| |
roots of a polynomial |
If 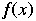 is a polynomial, the roots of is a polynomial, the roots of 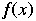 are those numbers c so that are those numbers c so that 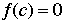 . . |
|
7 |
Quadratic Reciprocity |
|
|
| |
Legendre symbol |
|
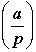 |
| |
Quadratic Recirocity |
|
Suppose that p and q are odd primes.
1. 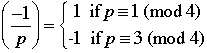
2. 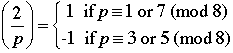
3. If 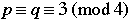 , then , then 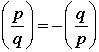 . .
4. If p or q or both 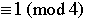 , then , then 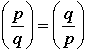 . . |
| Part Two |
Galois Theory and Representations |
|
|
8 |
Galois Theory |
|
|
| |
algebraic numbers |
A complex number is algebraic if it is the root of some Z-polynomial. |
|
| |
set of all algebraic numbers |
That subset of C which consists of all the equations 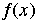 = 0 where = 0 where 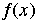 is a polynomial with integer coeficients. It can be shown that is a polynomial with integer coeficients. It can be shown that 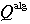 is a field. Note that i is an algebraic number (it is the solution to the equation is a field. Note that i is an algebraic number (it is the solution to the equation 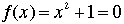 ). ).
Examples:
All the integers. (they are solutions for the polynomial equation x - n = 0 ).
All rational numbers. (they are solutions for the polynomial equation bx - a = 0 ).
nth roots of every fraction. ( they are solutions for the equation 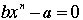 . . |
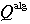 |
| |
algebraically closed field |
It can be shown that the sum, difference, product and quotient of any two algebraic numbers will also be an algebraic number.
p is not in 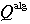 . (This is difficult to prove.) . (This is difficult to prove.)
It can be difficult to prove whether a particular number is or is not in 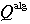 . .
There are lots of algebraic numbers and they are connected in many complicated ways. |
|
| |
absolute Galois group |
1. 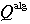 is the set of all complex numbers that can appear as roots of Z-polynomials. is the set of all complex numbers that can appear as roots of Z-polynomials.
2. The absolute Galois group G is made up of all permutations g of 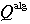 that preserve addition and multiplication. that preserve addition and multiplication.
3. If g is any element of G and f(x) is any Z-polynomial, then as g acts as a permutation of 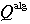 , it permutes the roots of f(x). It never maps some root of f(x) to a nonroot of f(x). , it permutes the roots of f(x). It never maps some root of f(x) to a nonroot of f(x).
4. G has infinitely many elements.
5. There is only one element of G, other than the neutral element e, for which we can give a complete description. This element is called c, the complex conjugate. No other element of G an be written down explicitly.
6. Any element g of G can be partially described by taking a Z-polynomial f(x), listing its roots 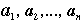 and telling what permutation of these algebraic numbers occurs when we apply g. and telling what permutation of these algebraic numbers occurs when we apply g.
7. Zorn's Lemma plus some advanced algebra can be used to piece together the partial descriptions of item 6 to get elements of G. That is how we know that G is infinite. |
G |
| |
Zorn's Lemma |
Allows us to compress the process of doing infinitely many things in a short amount of time, so that we can still have time left over. |
|
| |
symmetry |
A symmetry is a function that preserves what we feel is important about an object.
Each g in the Galois group G is a symmetry of 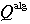 because it preserves the operations that concern us in algebra, namely, addition and multiplication. because it preserves the operations that concern us in algebra, namely, addition and multiplication. |
|
| |
|
|
|




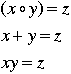
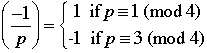
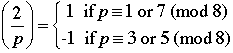
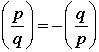 .
.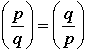 .
.