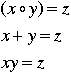Friday November 17, 2006 2:00 PM Lethbridge Sunrise 7:46 Sunset 17:47 Hours of daylight: 9:01
A. Morning Musings
2:00 PM (!) It is +7 C at the moment with a high of +9 C forecast.
I totally missed starting the day with a Web update. Better late than not at all.
|
|
From rear window |
South patio |
Both images taken at 2:00 PM |
B. Plan
| Immediate |
|
|
| Health |
Walk & exercise |
1 hr |
| Mathematics |
Make notes for "Fearless Symmetry" chap 8: Galois groups |
1 hr |
| History |
Continue reading & making notes for "Citizens" |
1 hr |
| GO |
Play 3 games of 9x9 GO++; Solve problems from Graded GO Problems for Beginners |
1 hr |
| Literature |
Begin reading "Disgrace" by Coetze |
1 hr |
| Later |
|
|
| Chores |
Investigate water softeners for home |
|
| Technology |
Read manual for cell phone |
|
| |
Make notes for chap. 4 of "Switching to the Mac" |
|
| |
Begin reading "iPhoto" |
|
| |
digital photography - learn about using the various manual settings |
|
| Philosophy |
Read "The Art of Living" by Epictetus |
|
| Mathematics |
Larson "Calculus" |
|
| |
Read "Symmetry" by Hermann Weyl |
|
| |
Read "The Computational Beauty of Nature" Chap
3 |
|
| |
Gardner "The Colossal Book of Short Puzzles" |
|
| History |
Watson "Ideas" |
|
| Model Trains |
Build oil refinery diorama: add ground cover |
|
| |
Assemble second oil platform kit |
|
| |
Assembly of CN 5930, an SD40-2 with a NAFTA logo |
|
| Puzzles |
The Orange Puzzle Cube: puzzle #9 |
|
C. Actual/Notes
I have maintained a little Literature, but Mathematics, History and GO have all taken a sabbatical. Time to pull up my socks.
|
Mathematics 19
November 17
|
|
Mathematics Chronology |
2:30 PM
I have read and reread "Fearless Symmetry" chap 8 Galois Groups a few times during the last week. Now to make a few notes. |
The book is divided into three main parts:
- Part One. Algebraic Preliminaries (chaps. 1 - 7)
- Part Two. Galois Theory and Representations (chaps. 8 - 16)
- Part Three. Reciprocity Laws (chaps. 17 - 23)
I am thoroughly enjoying this book. It is quite different than other books I have read in the last couple of years. I would categorize these books as follows:
- books that describe how to "do" certain things (e.g. textbooks)
- books on the history of mathematics
- general books on mathematics, but no "real" mathematics
- books that focus on the ideas and concepts of mathematics (this book!)
|
"Fearless Symmetry" is largely about terminology (i.e. concepts) and notation.
Let me try to review the previous seven chapters that constitute Part One:
Chapter |
Terminology (concepts) |
Notation |
| Part One |
Algebraic Preliminaries |
|
1 |
Representations |
|
|
set |
|
|
one-to-one correspondence |
|
|
standard object |
|
|
function |
|
|
morphism |
|
|
representation |
|
2 |
Groups |
|
|
group |
|
| |
group law |
|
| |
discrete groups |
|
| |
integers under addition |
|
| |
permutation group |
|
| |
continuous groups |
|
| |
Lie groups |
|
| |
rigid motions in space
|
|
| |
rotations of a circle
|
SO(2) |
| |
rotations of a sphere
|
SO(3) |
| |
set of real numbers under addition |
R |
3 |
Permutations |
|
| |
group of permutations |
|
| |
identity permutation |
e |
| |
cycle decomposition |
|
4 |
Modular Arithmetic |
|
| |
conguence |
|
| |
modulus |
|
| |
integer |
|
| |
prime number |
|
| |
field |
|
5 |
Complex Numbers |
|
| |
real number |
|
| |
complex number |
a + bi |
| |
complex conjugate |
a - bi |
| |
set of all complex numbers |
C |
| |
algebraic closure |
|
6 |
Equations and Varieties |
|
| |
rational number |
|
| |
irrational number |
|
| |
set of all rational numbers |
Q |
| |
Z-equation |
|
| |
set of all integers |
Z |
| |
set of integers modulo p |
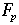 |
| |
variety |
|
| |
roots of a polynomial |
|
7 |
Quadratic Reciprocity |
|
| |
Legendre symbol |
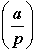 |
| |
Quadratic Recirocity |
Suppose that p and q are odd primes.
1. 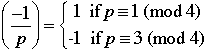
2. 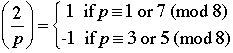
3. If 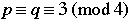 , then , then 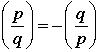 . .
4. If p or q or both 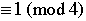 , then , then 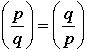 . . |
| Part Two |
Galois Theory and Representations |
|
8 |
Galois Theory |
|
| |
algebraic numbers |
|
| |
set of all algebraic numbers |
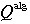 |
| |
algebraically closed field |
|
| |
absolute Galois group |
G |
| |
|
|
| |
|
|
I am not happy with the above table (yet). Although it identifies many of the important concepts that have been discussed so far, it fails to clarify exactly what these concepts are.
I need to add one more column that does this.
I also need to add at least one example to illustrate the nature of the concept. |
Chapter |
Terminology (concepts) |
Description |
Notation |
| Part One |
Algebraic Preliminaries |
|
|
1 |
Representations |
|
|
|
set |
A set is a collection of things, often called the elements of the set. |
{a, b, c} |
|
one-to-one correspondence |
A one-to-one correspondence from a set A to set B is a rule that associates to each element in A exactly one element in B, in such a way that each element in B gets used exactly once, and for exactly one element in A. |
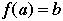
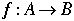
|
|
standard object |
This is an object that we know quite a bit about. |
|
|
function |
A function from a set A to a set B is a rule that assigns to each element in A an element of B. |
|
|
morphism |
A morphism is a function from A to B that captures at least part of the essential nature of the set A in its image in B. |
|
|
representation |
A representation is a morphism (i.e. a function) from a source object to a standard target object.
If A represents B, we have three things: two objects, A and B, which in this context will be sets, and the relation between them, which will be a morphism. When A and B have some additional "structure" (e.g. they are finite sets, or ordered sets, or ...) and we restrict the possible morphisms from A to B to have something to do with that structure. |
|
| |
Example:
Let A be the set {red, blue, yellow, pink}.
Let B be the standard object {1, 2, 3, 4}. Let f be the following rule: red is associated with 1, blue is associated with 2, yellow is associated with 3 and pink is associated with 4. f is a morphism because because this rule is capturing something about the number of elements in A. Therefore we may consider f to be a representation of A. |
2 |
Groups |
|
|
|
group |
A group G is a set with a composition defined on pairs of elements such that :
1. There is a neutral element e in G, so that 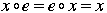 no matter what element in the group is substituted for x. e is sometimes called the identity element. no matter what element in the group is substituted for x. e is sometimes called the identity element.
2. For any element x of G, there is some element y in G so that 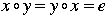 . That is, every element has an inverse element. . That is, every element has an inverse element.
3. For any three elements, x, y, and z in G, we have 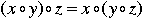 . This is called the associativity of the composition. Each group has its own law of composition. It can be whatever we define it to be (e.g. addition, multiplication, rotation, ...). . This is called the associativity of the composition. Each group has its own law of composition. It can be whatever we define it to be (e.g. addition, multiplication, rotation, ...). |
|
| |
group law |
If G is a group, the group law is the rule that tells how to combine two elements in the group to get the third. |
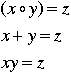 |
| |
discrete groups |
There is no smooth path from one element to another. (e.g. the integers) |
|
| |
integers under addition |
|
|
| |
permutation group |
|
|
| |
continuous groups |
There are infinitismal differences between elements. |
|
| |
Lie groups |
Pronounced "Lee", named after the Norwegian mathematician Sophus Lie who studied them. |
|
| |
rigid motions in space
|
|
|
| |
rotations of a circle
|
|
SO(2) |
| |
rotations of a sphere
|
|
SO(3) |
| |
set of real numbers under addition |
|
R |
| |
Examples:
Consider the set Z of all the integers (positive, negative and zero). Z is an infinite set. Let the group law be familiar addition. Then Z under this group law is a group.
Consider the set of three rotations of 60, 120 and 180 degrees of an equilateral triangle. The rotations constitute the group law. The elements of the group are the three positions (i.e. orientations) of the triangle.
Groups are used to describe various types of symmetries. |
3 |
Permutations |
|
|
| |
group of permutations |
|
|
| |
identity permutation |
|
e |
| |
cycle decomposition |
|
|
4 |
Modular Arithmetic |
|
|
| |
conguence |
|
|
| |
modulus |
|
|
| |
integer |
|
|
| |
prime number |
|
|
| |
field |
|
|
5 |
Complex Numbers |
|
|
| |
real number |
|
|
| |
complex number |
|
a + bi |
| |
complex conjugate |
|
a - bi |
| |
set of all complex numbers |
|
C |
| |
algebraic closure |
|
|
6 |
Equations and Varieties |
|
|
| |
rational number |
|
|
| |
irrational number |
|
|
| |
set of all rational numbers |
|
Q |
| |
Z-equation |
|
|
| |
set of all integers |
|
Z |
| |
set of integers modulo p |
|
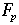 |
| |
variety |
|
|
| |
roots of a polynomial |
|
|
7 |
Quadratic Reciprocity |
|
|
| |
Legendre symbol |
|
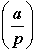 |
| |
Quadratic Recirocity |
|
Suppose that p and q are odd primes.
1. 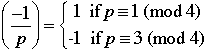
2. 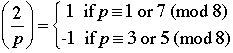
3. If 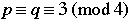 , then , then 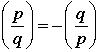 . .
4. If p or q or both 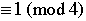 , then , then 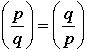 . . |
| Part Two |
Galois Theory and Representations |
|
|
8 |
Galois Theory |
|
|
| |
algebraic numbers |
|
|
| |
set of all algebraic numbers |
|
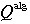 |
| |
algebraically closed field |
|
|
| |
absolute Galois group |
|
G |
| |
|
|
|
| |
|
|
|
|
D. Reflection |




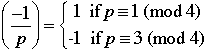
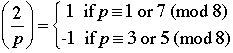
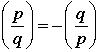 .
.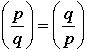 .
.