Sunday November 19, 2006 5:40 am Lethbridge Sunrise 7:49 Sunset 17:44 Hours of daylight: 8:55
A. Morning Musings
5:40 am It is 0 C at the moment with a high of +13 C forecast. It is about 10 degrees warmer than normal for this time of year.
This is better. I am back to my early morning routine.
Mathematics. I went into the uni library yesterday and borrowed the Rotman textbook "Advanced Modern Algebra". I am curious to see how the topic is presented at the graduate level.
|
|
From rear window |
South patio |
Both images taken at 12:00 PM |
B. Plan
| Immediate |
|
|
| Health |
Walk & exercise |
1 hr |
| Mathematics |
Read "Fearless Symmetry" chap 9: Elliptic Curves |
1 hr |
| History |
Continue reading & making notes for "Citizens" |
1 hr |
| GO |
Play 3 games of 9x9 GO++; Solve problems from Graded GO Problems for Beginners |
1 hr |
| Literature |
Continue reading "Disgrace" by Coetze |
1 hr |
| Later |
|
|
| Chores |
Investigate water softeners for home |
|
| Technology |
Read manual for cell phone |
|
| |
Make notes for chap. 4 of "Switching to the Mac" |
|
| |
Begin reading "iPhoto" |
|
| |
digital photography - learn about using the various manual settings |
|
| Philosophy |
Read "The Art of Living" by Epictetus |
|
| Mathematics |
Larson "Calculus" |
|
| |
Read "Symmetry" by Hermann Weyl |
|
| |
Read "The Computational Beauty of Nature" Chap
3 |
|
| |
Gardner "The Colossal Book of Short Puzzles" |
|
| History |
Watson "Ideas" |
|
| Model Trains |
Build oil refinery diorama: add ground cover |
|
| |
Assemble second oil platform kit |
|
| |
Assembly of CN 5930, an SD40-2 with a NAFTA logo |
|
| Puzzles |
The Orange Puzzle Cube: puzzle #9 |
|
C. Actual/Notes
|
Mathematics 21
November 19
|
|
Mathematics Chronology |
6:10 am
I am having a first look at Joseph Rotman's (2002) "Advanced Modern Algebra". |
Chapter 1 Things Past
- 1.1 Some Number Theory
- 1.2 Roots of Unity
- 1.3 Some Set Theory
This is my first experience with a graduate level textbook on modern algebra.
My first thought is to see if I can come up with a visual representation of the material using either MindManager or Inspiration software. Since I will be using considerable mathematical notation, I will have to use MathType to create the expressions and then see if I can import these into the appropriate diagrams.
The book begins with a number of definitions, axioms, propositions, theorems and corollaries. The challenge is to see if I can create a map that shows the relationships among these various entitities. The propositions, theorems and corollaries all require a proof. I will begin by ignoring the actual proofs and see if I can simply see the pattern of what has been developed. |
Here is a skeleton structure using Mindmanager:

I like using color, and to a lesser extent, shape, to identify the different types of information. This is a no-nonsense book. It is simply a list of important definitions, propositions, and theorems. In this chapter, which is considered to be a review, many of the proofs are just sketched out rather than rigorously proven.
One important issue it the relative importance of these proofs. Is that what Number Theory is really all about: a structure of rigorous definitions and proofs? Or is most of the topic understanding what the various theorems say and then moving on, until one arrives at an area that is close to original research?
My sense at the moment is that it is a little of both. It is probably a good idea to study some of the proofs for the more important theorems, and to skim over much of the rest.
Another issue is this way of making notes. The backbone software is Dreamweaver, which I am using to create these web pages. When should I switch to MindManager and work within that environment. In both cases I also need to use MathType to create mathematical expressions, and in both cases I can copy and paste images and text from MathType into Dreamweaver or MindManager.
I am going to stay with MindManager for a bit and see how that goes...
I recall using a table format within Dreamweaver as a template for proofs. Let's see if I can find a previous example. I recall that it was while studying the Spivak book on calculus. Nope. I couldn't seem to find a page that matched the template in my mind. An indication that my web site still needs some refinement.
Let me try rewriting the proof for Proposition 1.1 using a table format. |
Proposition 1.1 Every integer n > 1 is either a prime or a product of primes.
Proof:
| Step |
Description |
Reason |
1 |
Let C be the subset of N consisting of all those n > 1 for which the proposition is false. That is, C contains numbers that are not prime and not a product of primes. |
The goal is to show that C is the empty set. |
2 |
Assume C is nonempty. |
|
3 |
Then C contains a smallest integer, say, m. That is, m is a member of C. |
Least Integer Axiom |
4 |
Suppose m is not a prime |
|
5 |
Then m is not a product of primes. |
step 1 + step 4 |
6 |
Therefore there are natural numbers a and b with m = ab, a < m, and b < m |
|
7 |
Neither a nor b lies in C |
Both a and b are less than m, which is the smallest integer in C |
8 |
Therefore a and b are each either prime or a product of primes. |
|
9 |
Therefore m = ab is a product of (at least) two primes. |
Contradicts step 5 |
|
Therefore C is the empty set. |
|
2:20 PM I am back from the uni library with 3 book on abstract algebra:
- Abraham P. Hillman & Gerald L. Alexanderson. Abstract Algebra: A First Undergraduate Course. (1994). Fifth Edition.
- Robert B. Ash. (1998). A Primer of Abstract Mathematics.
- Joseph A. Gallian. (1990). Contemporary Abstract Algebra. Second Edition.
|
Here are a few quotes from Gallian that I enjoyed:
- "I agree with George Polya that guessing and conjecturing are important in mathematics and should be taught and encouraged wherever possible." [p. xi]
- "In my opinion, every undergraduate mathematics course should have a liberal arts character. I have tried to achieve this with comments, historical notes, quotations, biographies, and photographs, and in general, by my approach to the entire subject." [p. xi]
- "Several theorems are presented without proof. In each instance I feel that it is the understanding of the statement of the theorem, not its proof, that is the important issue." [p. x]
There are a number of issues to keep in mind as one Learns more about abstract algebra. One is to identify the theorems that appear to be the most important, and similarly, to identify the proofs that reveal the beauty of a proof. Another is to think of examples that illustrate the abstract theorems. Third, is to solve most of the exercises that are presented. Fourth, is to think of a few good questions about what one has Learned.
The zeroth chapter of the Gallian book is called Preliminaries [p. 3 - 20] |
Axiom: Well Ordering Principle
Every nonempty set of positive integers contains a smallest member.
This is self-evident. Think of any set of positive integers. For example {3,12, 2, 99}. Reorder the numbers from smallest to largest. Then the first number in the reordered set will be the smallest member. In this example, the reorderd set is {2, 3, 12, 99} and the smallest member is 2.
The principle also applies to any finite set of integers, positive, negative or zero, but it does not apply to the infinite set of all integers since there is no end to the number of negative integers and thus this set does not have a smallest number.
Definition: A nonzero integer t is a divisor of an integer s if there is an integer u such that s = tu.
Notation: In this case we write t | s and say "t divides s"
Definition: A prime is a positive integer greater than 1 whose only positive divisors are 1 and itself.
Theorem: Division Algorithm
Let a and b be integers with b > 0. Then there exist integers q and r with the property that a = bq + r where 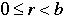 . .
Proof:
No |
Description |
Reason |
1 |
Consider the set S = {a - bk | k is an integer and 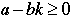 . . |
|
2 |
If 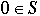 , then b divides a and we have q = a / b and r = 0. , then b divides a and we have q = a / b and r = 0. |
|
3 |
If 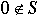 , and S is nonempty, then S has a smallest element, say r = a - bq , and S is nonempty, then S has a smallest element, say r = a - bq |
Well ordering principle |
4 |
Then a = bq + r and |
|
|
|
|
|
|
|
|
D. Reflection |




