Content
Prime Obsession. Chapter 1 Card Tick [p. 3 - 18]
The series 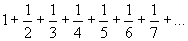 is called the harmonic series.
Theorem: The harmonic series is divergent (i.e. it sums to infinity).
Proof: (due to d'Oresme 1323 - 1382)
Consider grouping the terms by taking the first 2 terms, then the next 4 terms, then 8, then 16 and so on. Each group is greater than 1/2. Thus the series is greater than an infinite sum of fractions, each of which is greater than 1/2.
It is noteworthy that the proof depends on noticing a pattern among the possible ways of summing the series.
Now consider the series 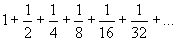 = 2. This series is said to be convergent.
I (vaguely) recall a section in one of my undergraduate textbooks that discussed how to determine if a series was divergent or convergent. I have just looked at the Larson text on Calculus and note that chapter 8 is devoted to sequences and series. There is a huge difference between reading about mathematics and doing mathematics. At the moment I am just reading about mathematics and seeing if I understand it.
Another interesting series is a variant of the harmonic series where the signs alternate between + and -. This series is convergent, and can be shown to converge to 2/3.
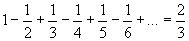
The study of infinite series used to be called analysis which is the theoretical framework for calculus. However the actual use of words such as infinity were dropped in the late nineteenth century in favor of phrases that simply involved terms like "less than" and "greater than".
Analysis today is usually thought of as the study of limits.
Derbyshire suggests that mathematics be thought of as 4 major subdisciplines:
- Arithmetic - the study of integers and rational numbers
- Geometry - the study of figures in space
- Algebra - the study of abstract symbols and rules for combining these symbols
- Analysis - the study of limits
Derbyshire then refers to the combining of arithmetic and analysis as "the great fusion" forming the new field of analytic number theory.
Prime Obsession. Chapter 2 The Soil. The Crop. [p. 19 - 31]
Bernhard Riemann's 1851 doctoral dissertation "is nowadays regarded as a classic of nineteenth-century mathematics, but it drew little attention at the time in spite of being enthused over by Gauss." [p. 31] In 1859 he submitted a short paper describing some research he was engaged in as part of his appointment to the Berlin Academy (a research institution). This paper was titled "On the Number of Prime Numbers Less Than a Given Quantity". This paper revolutionized mathematics and began the new field of analytic number theory.
I am about to search the web and see if I can locate this article. That only took a minute! Googling Riemann and "On the Number of Prime Numbers Less Than a Given Quantity" did it perfectly. Here is the document (translated). |
