Content
Prime Obsession. Chapter 3 The Prime Number Theorem [p. 32 - 47]
"The main idea of a function is that some number depends on some other number according to a fixed rule or procedure." Often this rule is expressed as a formula, but it is perfectly acceptable for it to be expressed verbally as a process.
The values that the function takes as inputs are referred to as the domain of the function, and the values it gives as outputs are called the range. Another common phrase is to say that a function is a way to map a number to another number.
Quite often there is a restriction that each value in the domain must map to a unique number in the range. Such functions are called single-valued, or if the context is clear, simply functions where it is taken for granted that they are single-valued. There is a special topic called multi-valued functions that deals with the more general case.
One function that is of special interest in number theory is called the Prime Counting Function. It is symbolized by p(N). For any value of N (a Natural number), it gives the number of prime numbers up to N (inclusive). This function is very interesting, in large part because there is no known formula for giving this number. There are a number of procedures for algorithmically going through the numbers and noting which ones are prime and then adding the number of such primes. The procedures themselves are a subtopic of investigation.
Two very important families of functions for Number Theory are the logarithmic and exponential functions. Therefore it is important to become very familiar with these two types of functions. This also involves the special number  , named for Leonard Euler. , named for Leonard Euler.
Another important idea is that of an inverse function. An inverse function is one that returns the argument to its original value. For example, division is the inverse of multiplication, subtraction is the inverse of addition, integration is the inverse of differentiation, and exponentiation is the inverse of logarithmization.
The Prime Number Theorem: 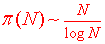
Note that the PNT is not an equation, but a statement about asymptotic approximation as N gets very large.
Using the fact that when dealing with all the numbers up to some large N, most of those numbers resemble N in size. This allows us to make a few more "approximate" statements:
The probability that N is prime is 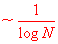
The N-th prime number is  . .
The above statements are examples of the general topic of the distribution of the prime numbers. This is a rich and open-ended topic that has attracted the interest of many famous mathematicians, including Gauss, Euler and Riemann.
Two noteworthing features of the distribution of prime numbers is :
- there is a thinning out of the prime numbers as N gets very large
- there is a certain quality of randomness to the distrubution.
Prime Obsession. Chapter 4 On the Shoulders of Giants. [p. 48 - 62]
Leonhard Euler (1707 - 1783) (Swiss) is the only mathematician to have two numbers named after him, one of which is the number  . Euler spent much of his adult life in St. Petersburg. Derbyshire calls one of Euler's discoveries "the Golden Key", although I am not sure at the moment what this is. . Euler spent much of his adult life in St. Petersburg. Derbyshire calls one of Euler's discoveries "the Golden Key", although I am not sure at the moment what this is.
Carl Frederich Gauss (1777 - 1855) (German) is recognized at the first person to see the truth of the Prime Number Theorem. One can spend hours browsing the Web looking at sites that discuss some aspect of Gauss's work.
|