1:00 PM Lethbridge, Alberta
I have just completed reading and yellow highlighting chapter 3 of the book "The Art of the Infinite: Our Lost Language of Numbers" by Robert & Ellen Kaplan (2003), pages 56 - 74. It is difficult to express the emotional feelings that I now have, having just finished the chapter. I have two goals. One is try to capture the important points of the chapter, the other is the excitement of playing with prime numbers.
Review
So far the Kaplans' book has mentioned the wide variety of numbers (e.g. rational, irrational, real, imaginary, complex, transcendental, ...) that we can create beginning with just the Natural numbers and the operations of addition and multiplication. They then spent a chapter reviewing the basic idea of mathematical proof. Chapter 3 is about prime numbers. |
| My next step will be to make a few notes about chapter three"Designs on a Locked Chest " [p. 56 - 74]. |
Content
There are a few proofs provided that show why the multiplication of two negative numbers is a positive. These proofs are fundamentally dependent on the wording of the axioms that one wishes to begin with. Peono's axioms are one such set, another are those provided by Spivak in his calculus book.
Theorem: The number of primes in infinite.
Proof by contradiction (Euclid):
Assume there are a finite number of primes, p.
Create a new number n = 2 x 3 x 5 x 7 x 11 x ... x p
Now consider the number n + 1.
n + 1 cannot be divided by any of the primes between 2 and p since division by any of them would leave a remainder of 1. Thus n + 1 is either a prime or there is another number q between p and n + 1 that is prime. Either way we have found a prime greater than p, which contradicts our initial assumption.
Theorem: There are strings of numbers as long as you like that haven't a single prime in them.
Proof:
Think of a number n. Then create the number n! (n factorial: 2 x 3 x 4 x 5 x 6 x ... x n)
Now consider the string of consecutive numbers n! + 2, n! +3, n! + 4, ... n! + n. None of these n - 1 numbers can be prime since the first is divisible by 2, the next by 3 and so on.
Conjecture: There are an infinite number of twin primes (i.e. two prime numbers that differ by 2)
There is no known proof, although most mathematicians believe this is likely true.
Theorem: Any sequence of the form an + b will have infinitely many primes in it as n goes through the Natural numbers.
Proof: Direchlet in 1837.
Special Function: p(x) = number of primes less than or equal to x.
Gauss found two functions that closely approximate p(x). One was 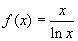 . The other was . The other was 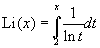 . .
It is surprising that logarithms and exponential functions appear in a discussion of prime numbers which only involve the Natural numbers. This is likely because the actual object being considered is a distribution rather than a simple arithmetic extension of the Natural numbers.
The length of the largest prime-free gap up to the number x - call this g(x) - is well approximated by 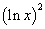 . .
End of chapter 3. [p. 74]
I have three books on my shelf about prime numbers and the Riemann Hypothesis that I would now like to look at:
- The Music of the Primes (2003) by Marcus du Sautoy.
- Prime Obsession (2003) by John Derbyshire.
- Stalking the Riemann Hypothesis (2005) by Dan Rockmore.
The Derbyshire book has more equations and looks like the one I would like to try first. The other two books may be more interesting for the historical background and context. But I may change my mind after seeing the Derbyshire in more detail.
|
| Here are a few quotes from "The Art of the Infinite: Our Lost Language of Numbers" that I enjoyed: |
Quotation |
Comment |
| "The tower of mathematics is inverted, widening up and outward from its few axioms." [p. 56] |
|
| "Further along this first tier lies the answer to a puzzle that has put too many people off math forever, convinced that its dicta were arbitrary or spiteful: for why should the product of two negative numbers be positive?" [p. 57] |
Realizing that this is a direct logical consequence of the elementary axioms of arithmetic is an important insight. However in order to see this one needs to understand the nature of a mathematical proof. |
| "Have negative numbers definitely moved mathematical thought into abstraction, where the dance of symbols becomes vivid instead of figures? Or do you find the visual proof in the appendix to this chapter not only convincing but illuminating?" [p. 59] |
But even the dance of the symbols has a visual aspect to it. |
| "It is as if the predominance in our brains of the visual cortex masked a different, deeper apprehension - of time, then, or something akin to music: structure itself." [p. 59] |
The visual cortex has strong evolutionary threads. Abstract thought is relatively recent in comparison, but may now turn out to be the critical feature for continued survival. |
| "What are the building blocks of multiplication? The composite number 24 breaks down into a sum of 1s, but a product of what - 2 and 12, or 3 and 8, or 4 and 6? If you look for the atomic factors of 24 you end up with 2x2x2x3. These factors are the atoms of multiplication because no further factor divides them. They are called the prime numbers." [p. 59 - 60] |
|
| "The twentieth century mathematician Paul Erdos often spoke of 'The Book': the book, he meant, in which God keeps all the most beautiful proofs. 'You don't have to believe in God,' said Erdos, 'but you do have to believe in The Book.' " [p. 61] |
Lovely! |
| "... that English put-down, 'a Beta mind' " [p. 62] |
|
| "After having so triumphantly proved so long ago that there are infinitely many primes, why are we having such trouble in the twenty-first century answering this simple question about their distribution? Perhaps our approach has been wrong." [p. 64] |
|
| "We proudly think: where pattern is, our minds will find it. What if after all, then, there is no pattern, and multiplication, unlike addition, is built - built by us! - on utterly chaotic foundations? |
How could one develop a proof by contradiction, or construct an example, that begins with the assumption that there is no pattern?
One example of a number that has no pattern is an irrational number. Is this a possible starting point? |
| "Since intuition and common sense have left us stranded, we need an insight - and then a proof for it to nestle comfortably into." [p. 67] |
|
| "[Gauss] mull over a question with a statistical flavor: ignoring the stuttering way they pop-up, might there yet be some regularity in how the sheer number of primes increases?" [p. 68] |
This is a different type of question. We are no longer looking at individual numbers, but instead are examining trends of large numbers of primes. |
| "Knowing what creatures there are and what creatures there could be in this crowd of primes must surely give us a presentiment of its structure, and some corner of the pattern may be the key that will turn it into a living garden, where what is design will sort itself out from ornament." [p. 74] |
I like the distinction between design and ornament. |
This chapter is exciting for the both the theorems it provides as well as for the many unanswered questions that it poses. |
2:50 PM
Total elapsed time: 1 hr 50 min.
3:35 PM Out of curiousity, I am about to search the amazon.com website for books on Number Theory.
Fascinating! There are numerous books out there on the topic. I will have another look at this after I have read my three books.
3:50 PM
Total elapsed time for the day: 2 hr 05 min
|


