Content
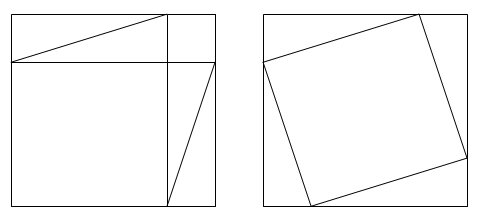
The authors give an example of a "proof" of the Theorem of Pythagorus that simply involves looking at two diagrams.
They follow this with a proof that the sum of n integers is 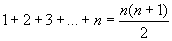 by simply pairing the first and last numbers of the sequence and showing that there are n/2 such pairs each of which adds to (n+1). These are both examples of a geometric approach to proof. The latter may also be proven using mathematical induction, which is an algebraic approach to proof.
The Greeks then came up with the idea of proof, to use as tight a system of logic as possible to substantiate the various relationships that they had noticed.
Descartes (1619) continued this tradition by stating that one must "begin with what we can intuit clearly and immediately". The Englishman John Locke took the opposite approach by beginning with reality and looking for "self-evident" truth. The German Immanuel Kant then elaborated on this idea by stating that we begin with perception, but that such perceptions are initially shaped by our intuitions of space and time. Thus mathematics is fundamentally about the logical conclusions that follow from our apriori ideas of space and time.
The axioms of mathematics were then refined during the eighteenth and nineteenth centuries as we became more adept at clarifying our ideas and concepts. The basic axioms for the natural numbers included the ideas of associativity and commutativity. Formalism, where the focus was on the relationships among the symbols, and where the symbols need not refer to anything in particular, became popular. However this approach eventually led, in the case of geometry, to a number of different geometries (depending on a basic assumption of parallel lines). However in the case of the natural numbers such formalism appeared to hold and provide a clear logical basis for the theorems about these numbers.
Eventually numbers became to be subsumed under the more general idea of sets, and set theory became the fundamental foundation for arithmetic. Richard Dedekind (1858) developed the idea that an irrational number could be conceptualized as what one has when one divided the numbers into two distinct sets where all of the members of one set are less than all the members of the other set. Such a cut is now referred to a Dedekind cut.
The Italian mathematician Giuseppe Peano developed the five key axioms that define the natural numbers which includes the idea of mathematical induction.
The German David Hilbert focused on trying to show that Peano's axioms were both consistent and complete. But in 1931 an Austrian mathematician Kurt Godel showed that no proof of consistency and completeness could ever be made within the system to which it referred.
At the moment there is less interest in pursuing the foundations of mathematics. Instead we are focusing on developing new theorems that simply show stunning patterns, relationships and results that are both useful and aesthetically pleasing.
End of chapter 2. [p. 55] |
