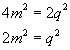Content
The Natural numbers consist of the positive integers beginning with the number one, and for each number there is a successor, created by adding one to that value.
However it is also natural to think of the result of taking something away from a collection. This might be sheep or sheckels. If I have four sheep and I give you one sheep, then how many sheep do I have left? At first the idea of taking a large number from a smaller number was simply forbidden as not making any sense, but in the world of commerce this was quickly incorporated into the idea of owing or of having a debt. This led, eventually, to the idea of negative numbers, and to the mathematical idea of subtraction. Further development involved the idea of the number zero, and the entire collection of positive integers, negative integers and zero were referred to as the Integers and were represented by the letter Z (from the German word for number, Zahl). At this point we have an infinite collection of numbers and two operations, addition and subtraction.
Although the exact history of the evolution of the concept of number to include the operations of multiplication and division will never be known with any certitude, we are able to see the consequences of such operations. Importantly, the operation of division gives rise to a new kind of number, now called a rational number. The collection of all rational numbers is represented by the letter Q (for quotient). A rational number is defined as the result of dividing one integer by another, where the special case of division by zero is not allowed. Such rational numbers have a number of interesting properties.
Theorem: Between any two rational numbers lies another.
Proof: Let 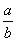 and and 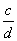 be any two rational numbers, where the first number is less than the second. That is, be any two rational numbers, where the first number is less than the second. That is, 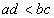 . .
Create a new number which is the average of the two numbers.
Then 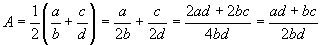 , which is also a rational number since a,b,c, and d are all integers. , which is also a rational number since a,b,c, and d are all integers.
It remains to show that 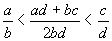 . .
Multiplying all terms by 2bd gives
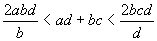
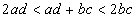
which is true since 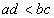 . .
This obvious property of the rational numbers is stunning. It is saying that no matter how close together I have two rational numbers, there is always room for another that is between them. In fact it is now easy to see that there are an infinity of such numbers since there are an infinite number of ways of creating such an intermediate number. This is sometimes expressed by saying that the rational numbers are dense on the number line.
Theorem: There exist numbers that are not rational.
Proof: Consider a right triangle with sides of length 1. Then the length of the hypotenuse is not a rational number.
This may be proved my contradiction. That is, assume that the length of the hypotenuse is a rational number that has been reduced so there are no common factors: 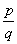 .
.
Then 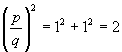 . .
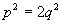 . That is . That is 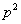 is an even integer, and thus p is also an even integer. Let it be 2m. is an even integer, and thus p is also an even integer. Let it be 2m.
Then 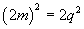 , and , and
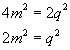
Therefore q is also an even integer, contradicting the original assumption. Thus this number (which we symbolize as 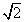 ) is not a rational number. We call such a number irrational. It is relatively easy to show that there are an infinite number of such irrational numbers as well. ) is not a rational number. We call such a number irrational. It is relatively easy to show that there are an infinite number of such irrational numbers as well.
Notation: Rational numbers may also be expressed using a decimal notation. Any such rational number will then have an expression that is either finite (e.g. 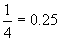 ) or which repeats in an endless cycle (e.g. ) or which repeats in an endless cycle (e.g. 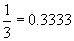 ). This leads to the conclusion that if one knows that a number has a nonrepeating decimal expansion then it must be irrational. ). This leads to the conclusion that if one knows that a number has a nonrepeating decimal expansion then it must be irrational.
There are an infinite number of easy ways to create an irrational number. Simply give a rule for writing the denominator that is an infinite nonrepeating number.
The collection of all the rational and irrational numbers are called the Real numbers, and are represented by the letter R.
The idea of taking the square root of a negative number gives rise to another kind of number, called imaginary and to the more general idea of a complex number, represented by the letter C. Such a number is not positive, since a positive times a positive is still positive, and it is not negative since a negative times a negative is also positive, and it is not zero. Therefore it does not lie on the Real number line. We currently represent this by means of another line that intersects the Real number line at zero.
It is difficult not to become excited by the richness of these number types and of their properties.
End of chapter 1. [p. 28] |
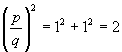 .
.