Nontrivial degeneracies of the particle in a two-dimensional box

Marc R. Roussel

Department of Chemistry and Biochemistry

University of Lethbridge

Let us start by defining the wavefunction:

>	psi := (nx,Lx,x,ny,Ly,y) -> 2/sqrt(Lx*Ly)*sin(nx*Pi*x/Lx)*sin(ny*Pi*y/Ly);

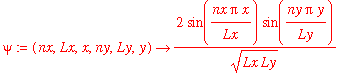
For Lx=Ly=L, there is a nontrivial degeneracy when nx^2+ny^2=50 since

1^2+7^2 = 5^2+5^2 = 50. We want to plot the corresponding wavefunctions to see what they look like. There are at least two sensible ways to do this. If you're working on a computer terminal, you can use plot3d, which allows you to manipulate the graph in real time (rotate it, add axes, etc.):

>	plot3d(psi(7,1,x,1,1,y),x=0..1,y=0..1,numpoints=50^2);

Note that we arbitrarily set L=1 for plotting. The "numpoints" option isn't strictly necessary, except that the default (25x25 grid points) isn't quite enough to plot this function accurately. To rotate the figure, just click and drag. To add axes, play with the coloring, etc., you can click on the figure and then use the buttons which appear in the tool bar, or you can right-click and select options from the drop-down menu which appears. Try it!

Sometimes, it's a little more convenient to look at a contour plot. This is like looking straight down at the figure. Where the contours are close together, the function is very steep. Color can also be used to specify depth above or below zero.

The following command loads up some extra plotting tools, including a contour plotter:

>	with(plots):

Warning, the name changecoords has been redefined

In the following plot, the blue regions are low (negative wavefunction) and the red regions are high (positive). (That's what the "coloring" option controls.)

>	contourplot(psi(7,1,x,1,1,y),x=0..1,y=0..1,numpoints=50^2,coloring=[blue,red],title="Particle in a square box, nx=7, ny=1");

>	contourplot(psi(5,1,x,5,1,y),x=0..1,y=0..1,numpoints=50^2,coloring=[blue,red],title="Particle in a square box, nx=ny=5");

These two quite different wavefunctions have exactly  the same energy.

Once we have two wavefunctions with the same energy, we can create other ones by superposition . For instance,

>	psi_new := (L,x,y) -> (psi(7,L,x,1,L,y) + psi(5,L,x,5,L,y))/sqrt(2);

is also a wavefunction with an energy of 50h^2/(8mL^2). The factor of sqrt(2) is a normalization factor:

>	int(int(psi_new(L,x,y)^2,x=0..L),y=0..L);

What does this new wavefunction look like? Let's have a look:

>	contourplot(psi_new(1,x,y),x=0..1,y=0..1,numpoints=50^2,coloring=[blue,red],title="Mixed wavefunction for the particle in a square box");

It is not necessary for the box to be square in order to have nontrivial degeneracies. The isolve function can help us find degeneracies. Suppose that we have Lx=3Ly. Then there are degeneracies if (nx/3)^2+ny^2=e has two different solutions, where e is an integer. We basically find degeneracies by trial-and-error, trying different values of e:

>	isolve((nx/3)^2+ny^2=2);

Since positive and negative quantum numbers are the same in the particle-in-a-box problem, there's really only one solution here, namely (nx,ny) = (3,1).

>	isolve((nx/3)^2+ny^2=4);

There are two distinct solutions here, but both have a zero quantum number, which isn't allowed.

>	isolve((nx/3)^2+ny^2=5);

Here we have two physically realistic, distinct solutions: There will be a degeneracy for the following pairs of quantum numbers: (nx,ny) = (6,1) or (3,2). Let's look at those wavefunctions.

>	contourplot(psi(6,3,x,1,1,y),x=0..3,y=0..1,numpoints=50^2,coloring=[blue,red],title="Particle in a rectangular box, nx=6, ny=1",scaling=CONSTRAINED);

Note the adjustment in Lx, both in the wavefunction and in the x  plotting range. The "scaling" option forces the two axes to be plotted in proportion.

>	contourplot(psi(3,3,x,2,1,y),x=0..3,y=0..1,numpoints=50^2,coloring=[blue,red],title="Particle in a rectangular box, nx=3, ny=2",scaling=CONSTRAINED);

Again we see an example of two quite different quantum states with exactly the same energy.