The energy of a photon is related to its momentum by
It turns out that Ce has a ground-state electronic configuration of [Xe]4f15d16s2. The reason why this atom has 3+ and 4+ ions is now a little clearer: The 3+ ion probably has a [Xe]4f1 configuration while the 4+ ion has a simple [Xe] electronic configuration.
You can see from this example why I didn't make a big deal of the lanthanides and actinides in class: Their chemistry is really quite complex.
The
p1 and
p-1 orbitals are tori. If
we add two such orbitals (one from each atom), we get a
cylindrical molecular orbital with a nodal line (a region of
depressed electron density) along the bond
axis. These are ![]() orbitals.
orbitals.
The bond order would be (10-9)/2 = 1/2. The nonzero bond order indicates a stable molecular ion. The unpaired electron in the
- (a)
- The reduced mass is
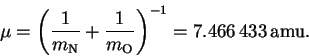
Since an amu is a g/mol, we have
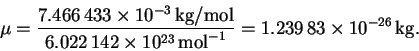
The frequency is
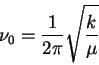
so that
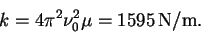
- (b)
- The reduced mass of
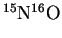 is 7.740774amu, or
is 7.740774amu, or
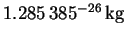 .
The fundamental vibration
frequency is then
.
The fundamental vibration
frequency is then
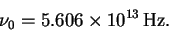
- (a)
- The energy of one 680nm photon is
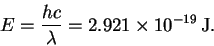
The energy of a mole of such photons is therefore 176kJ. Note that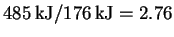 so that it
takes 3mol of 680nm photons to fix 1mol of carbon.
so that it
takes 3mol of 680nm photons to fix 1mol of carbon.
- (b)
- The quantum yield is about 1/3.
- (a)
- The mean rotational splitting is 12.1627GHz which,
converted to energy units, is
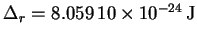 .
This is an absorption spectrum, so the rotational
splitting is
.
This is an absorption spectrum, so the rotational
splitting is 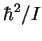 .
Thus
.
Thus
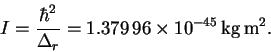
- (b)
- The photon energies are given by
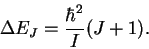
Note that the J in this equation is the initial value of the quantum number and that during absorption, this quantum number increases. (GHz)
(GHz) (10-23 J)
(10-23 J)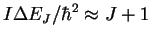
transition 24.32592 1.611852 2 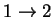
36.48882 2.417774 3 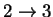
48.65164 3.223691 4 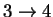
60.81408 4.029583 5 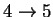
- (c)
- The exciting line has a frequency of 890300GHz.
The Raman spectrum has lines at
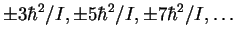 relative to the
exciting radiation. The quantity
relative to the
exciting radiation. The quantity 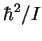 ,
converted
to frequency units, is 12.1627GHz.
Thus the frequencies of the
rotational Raman lines are (in GHz) 890264, 890239,
890215, ...and 890336, 890361, 890385,
...
,
converted
to frequency units, is 12.1627GHz.
Thus the frequencies of the
rotational Raman lines are (in GHz) 890264, 890239,
890215, ...and 890336, 890361, 890385,
...