- (a)
- Suppose that electrons, each with a kinetic energy of
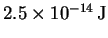 ,
are fired into a copper anode of
volume
,
are fired into a copper anode of
volume
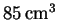 (volume measured at
(volume measured at
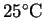 )
at a rate of
)
at a rate of
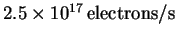 .
The anode is
hollow1 and
contains
.
The anode is
hollow1 and
contains
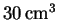 of water (measured at
of water (measured at
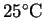 ). The anode and water are in good
thermal contact. If all the kinetic energy were
transformed to heat and assuming that none of the heat
is lost to the surroundings, how long would it take for
the anode's temperature to increase to
). The anode and water are in good
thermal contact. If all the kinetic energy were
transformed to heat and assuming that none of the heat
is lost to the surroundings, how long would it take for
the anode's temperature to increase to
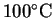 from 25? The density of copper at
from 25? The density of copper at
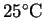 is
is
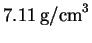 and its
specific heat capacity is
and its
specific heat capacity is
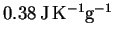 .
[8 marks]
.
[8 marks]
- (b)
- To avoid excessive heating of the anode, the water it
contains is constantly replaced by cool water.
Suppose that water with an initial temperature of
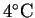 flows through the anode at a rate of
6L/min. Assuming perfect mixing of the water in the
anode and perfectly efficient heat transfer between the
copper and water, what steady temperature would the
anode reach? [7 marks]
flows through the anode at a rate of
6L/min. Assuming perfect mixing of the water in the
anode and perfectly efficient heat transfer between the
copper and water, what steady temperature would the
anode reach? [7 marks]
Hint: How much heat must be removed to hold the temperature steady?
Note: The temperature you will calculate here is a lower bound since neither mixing nor heat transfer will be perfectly efficient in the real system.
- (a)
- In deriving the equation for the energy of a particle in a box,
we assumed that the kinetic energy could be treated classically.
We can use the relativistic relationship between energy and
momentum instead to obtain an equation for a relativistic
particle in a box. Carry out this derivation.
[8 marks]
Hint: Except for the energy-momentum relation, the derivation is in all respects identical to that for the ordinary particle in a box.
- (b)
- Using the equation derived in question 2a, calculate the wavelength of a photon capable of inducing a transition from the ground state to the first excited state of an electron in a 3pm box. [7 marks]