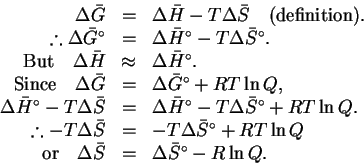The standard free energy change is therefore

From the pressures of CO and of H2, we obtain
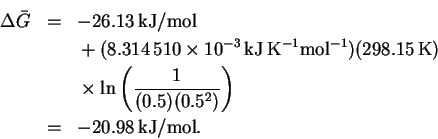
Since the free energy change is negative, the reaction would be spontaneous. There is therefore no thermodynamic reason why this would not work.
- (a)
- Since the reaction is isothermal and electrical work
is clearly not pressure-volume work, we want to calculate the
change in Gibbs free energy. The reaction is
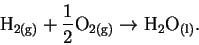
For this reaction,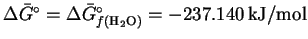 .
The activity of oxygen is
.
The activity of oxygen is
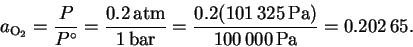
Similarly,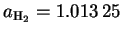 .
Therefore
.
Therefore
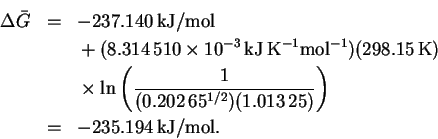
The molar mass of molecular hydrogen is 2.02g/mol, so
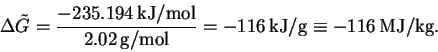
The maximum work is therefore 116MJ/kg. - (b)
- To calculate the free energy change at different
temperatures, we need
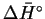 and
and
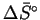 .
Using a thermodynamic table, we
find
.
Using a thermodynamic table, we
find
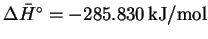 .
Therefore
.
Therefore
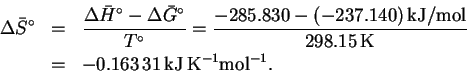
Accordingly,

The odd notation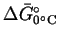 indicates that this
indicates that this
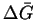 corresponds to
standard conditions (reactants and products at unit
activity), except for the temperature.
The rest of the calculation is identical to that in
question 2a:
corresponds to
standard conditions (reactants and products at unit
activity), except for the temperature.
The rest of the calculation is identical to that in
question 2a:
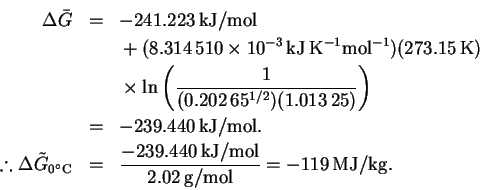
The calculation at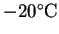 is identical:
is identical:
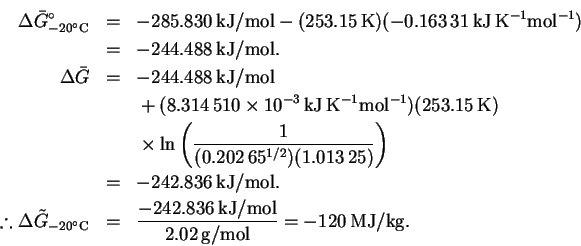
The maximum work is 119MJ/kg at 0 and 120MJ/kg at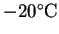 .
A heating system is therefore not
required from the point of view of efficiency,
but would be required to prevent the
aqueous medium from freezing.
.
A heating system is therefore not
required from the point of view of efficiency,
but would be required to prevent the
aqueous medium from freezing.