- (a)
- The reaction is
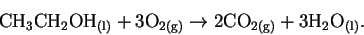
There is a decrease in the number of moles of gas. Moreover, ethanol can form only one hydrogen bond while three water molecules can be involved in multiple hydrogen bonding interactions. Both of these factors indicate an increase in the organization of the products relative to the reactants and so a decrease in entropy. - (b)
-
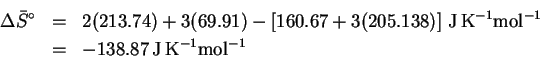
- (c)
- We would have to adjust the entropies of the reagents and
products to the new temperature. This is done by adding
the entropy at
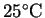 to the change in
entropy associated with heating each substance to
to the change in
entropy associated with heating each substance to
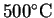 .
For water and ethanol,
we would need to calculate the change in entropy on
warming the liquid to the boiling point, the entropy of
vaporization at the boiling point and the change in
entropy on warming the vapor to the final temperature.
For oxygen and carbon dioxide, we would only need to
calculate the entropy change on warming these gases from
.
For water and ethanol,
we would need to calculate the change in entropy on
warming the liquid to the boiling point, the entropy of
vaporization at the boiling point and the change in
entropy on warming the vapor to the final temperature.
For oxygen and carbon dioxide, we would only need to
calculate the entropy change on warming these gases from
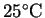 to
to
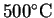 .
Accordingly, we would need the following data:
.
Accordingly, we would need the following data:
- the entropies at
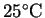 (from the table in
question 2b)
(from the table in
question 2b)
- the boiling temperatures of water and of ethanol
- the heats of vaporization of water and of ethanol at their respective boiling points
- the specific heat capacities of ethanol and water in both the liquid and vapor phases, of oxygen and of carbon dioxide
- the entropies at
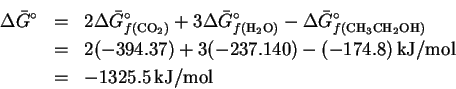
Since