Chemistry 2720 Fall 2000 Assignment 2 Solutions

1.

We begin by computing the molar enthalpy change. The reaction is

$$\mathrm{CO_{2(g)}} + \mathrm{H_2O_{(l)}} \rightarrow \mathrm{H_2CO_{3(aq)}}.$$

Therefore

$$\begin{eqnarray*}\Delta\bar{H}^\circ & = & \Delta\bar{H}^\circ_{f(\mathrm{H_2CO_... ...93.51 + (-285.830)]\,\mathrm{kJ/mol} = -20.36\,\mathrm{kJ/mol} \end{eqnarray*}$$

The number of moles of CO₂ is

$$n = \frac{20\,\mathrm{g}}{44.01\,\mathrm{g/mol}} = 0.4544\,\mathrm{mol}.$$

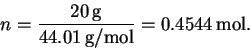
The total enthalpy change is therefore

$$\Delta H^\circ = n\Delta\bar{H}^\circ = -9.3\,\mathrm{kJ}.$$

2.

(a)

We worked out the equation for the work done during the reversible, isothermal expansion of an ideal gas in class:

$$\begin{eqnarray*}% latex2html id marker 29 w & = & -nRT\ln\left(\frac{V_2}{V_1}\... ...{-1}})(273\,\mathrm{K})\ln 20\\ & = & -6.80\,\mathrm{kJ/mol}. \end{eqnarray*}$$

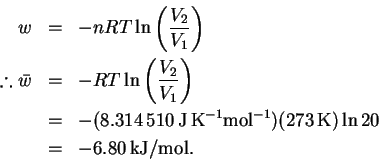
Note that this is an expansion so the work is negative (work done by the system).

(b)

The work per mole is calculated by

$$\bar{w} = -\int_{\bar{V}_1}^{\bar{V}_2}P\,d\bar{V}$$

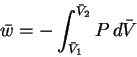
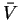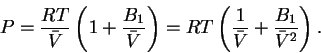
To do the integral, we must first write P as a function of $\bar{V}$:

$$P = \frac{RT}{\bar{V}}\left(1 + \frac{B_1}{\bar{V}}\right) = RT\left(\frac{1}{\bar{V}} + \frac{B_1}{\bar{V}^2}\right).$$

Thus

$$\begin{eqnarray*}\bar{w} & = & -RT\int_{\bar{V}_1}^{\bar{V}_2}d\bar{V}\left(\fra... ...mathrm{m^3/mol}}\right)\right]\\ & = & -6.79\,\mathrm{kJ/mol} \end{eqnarray*}$$

The correction hardly has any effect on the calculated value of the molar work.

3.

There are three possibilities:

(a)

The block is so hot that it will vaporize all the water. The final temperature will be greater than $100^\circ\mathrm{C}$.

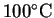(b)

The block is hot enough to vaporize only some of the water. The final temperature will be exactly $100^\circ\mathrm{C}$.

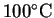(c)

The block is not hot enough to raise the temperature of the water to 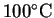$100^\circ\mathrm{C}$. All the water remains in the liquid state.  

We first need to decide which of these will be the case. To raise the temperature of the water from 20 to $100^\circ\mathrm{C}$ requires

$$q_{\mathrm{water,}20\rightarrow 100^\circ\mathrm{C}} = (800\... ...,\mathrm{J\,K^{-1}g^{-1}})(80\,\mathrm{K}) = 268\,\mathrm{kJ}.$$

We have

$$n_\mathrm{Fe} = \frac{300\,\mathrm{g}}{55.85\,\mathrm{g/mol}} = 5.37\,\mathrm{mol}.$$

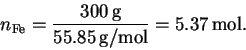
The heat released as the iron block cools from 150 to $100^\circ\mathrm{C}$ is therefore

$$q_{\mathrm{Fe,}150\rightarrow 100^\circ\mathrm{C}} = (5.37\,... ...thrm{J\,K^{-1}mol^{-1}})(-50\,\mathrm{K}) = -6.7\,\mathrm{kJ}.$$

Far more heat is required to raise the temperature of the water to $100^\circ\mathrm{C}$ than is available from cooling the iron to this temperature. Possibility 3c is therefore the correct one. We now have a straightforward heat balance problem:

$$\begin{eqnarray*}% latex2html id marker 109 q = 0 & = & \left\{\textrm{warm wate... ...0^\circ\mathrm{C})\\ \therefore T_f & = & 25^\circ\mathrm{C}. \end{eqnarray*}$$

4.

The reaction

$$\mathrm{NaOH_{(s)}} \rightarrow \mathrm{Na^+_{(aq)}} + \mathrm{OH^-_{(aq)}}$$

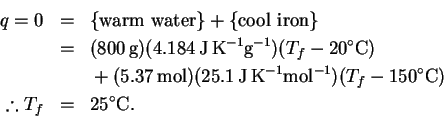
will either produce or absorb heat, leading to a change in temperature of the water. The molar enthalpy of reaction is

$$\begin{eqnarray*}\Delta\bar{H}^\circ & = & \Delta\bar{H}^\circ_{f(\mathrm{Na^+})... ...30.015) - (-425.6)\,\mathrm{kJ/mol} = -44.755\,\mathrm{kJ/mol} \end{eqnarray*}$$

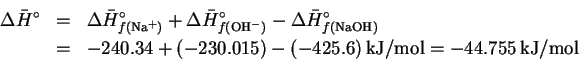
The number of moles of sodium hydroxide is

$$n_\mathrm{NaOH} = \frac{25\,\mathrm{g}}{40.00\,\mathrm{g/mol}} = 0.625\,\mathrm{mol}.$$

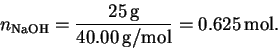
Thus

$$\Delta H^\circ = n\Delta\bar{H}^\circ = -27.97\,\mathrm{kJ}.$$

The reaction is exothermic, so the temperature will increase. We will need to do a computation with the heat capacity of water to determine the temperature rise. Molar and mass-specific heat capacities are available, so we need to convert the volume to one or the other set of units. Using the density of water at $25^\circ\mathrm{C}$, we find

$$m_\mathrm{H_2O} = (200\,\mathrm{mL})(0.9971\,\mathrm{g/mL}) = 199.4\,\mathrm{g}.$$

The heat balance equation is

$$\begin{eqnarray*}% latex2html id marker 148 q = 0 & = & \left\{\textrm{water war... ...0^3\,\mathrm{J})\\ \therefore \Delta T & = & 33.5\,\mathrm{K} \end{eqnarray*}$$

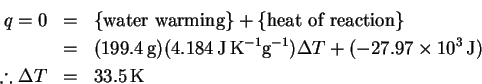
This is not so large a temperature change as to make this process very dangerous (the final temperature will be well below the burn temperature for human skin), but it will clearly be necessary to stir the solution as we go to avoid creating hot spots due to slow diffusion of the heat away from the site of dissolution.