


Up: Back to the Chemistry 2710 assignment
index
Chemistry 2710 Spring 2000 Practice Problems
- 1.
- The vibrational frequency of carbon monoxide is
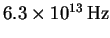 .
.
- (a)
- Calculate the difference in energy between any two
adjacent vibrational energy levels.
- (b)
- Calculate the ratio of the populations of adjacent
vibrational levels at 298K.
- (c)
- Because the vibrational spacing is (roughly) constant,
we can calculate the probability that a molecule
occupies the lowest energy level directly. Suppose that
the population ratio calculated in question
1b is f. Then,
N1 = fN0,
N2 = fN1
= f2N0, etc. The total number of molecules in all
energy levels is therefore
The infinite sum above can be shown to have the value
Therefore,
the probability that any given molecule occupies the lowest
energy level is
Calculate the probability that a carbon monoxide
molecule is in the lowest vibrational energy level at
298K.
- (d)
- Use the equipartition principle to estimate the average
total energy of a carbon monoxide molecule. The
experimental result is
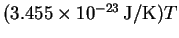 to T near 298K. How does the
equipartition value compare?
to T near 298K. How does the
equipartition value compare?
- 2.
- In the Diels-Alder reaction of ethene with 1,3-butadiene to form cyclohexene
in the gas phase,
the activation energy is 115kJ/mol. The following thermochemical
data for the reactants and products are available:
| Species |
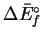 (kJ/mol)
(kJ/mol) |
|
C2H4(g) (ethene) |
54.95 |
|
C4H6(g) (1,3-butadiene) |
115.4 |
|
C6H10(g) (cyclohexene) |
14.24 |
- (a)
- Sketch the energy profile of the reaction. Clearly label
the
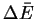 for the reaction as well as the activation
energies for the forward and reverse reactions.
for the reaction as well as the activation
energies for the forward and reverse reactions.
- (b)
- Calculate the activation energy for the reverse reaction
(
 ).
).
- (c)
- Calculate the enthalpies of activation for the forward and
reverse reactions at 298K.
- 3.
- The enthalpies of formation of ethane (
C2H6) and
of methyl radicals (
CH3) are, respectively,
-83.85 and 145.69kJ/mol at 298.15K. Calculate the activation energy for the
dissociation of ethane into methyl radicals.
Hint: Sketch the expected energy profile for this reaction.
- 4.
- Azomethane (
CH3N2CH3) decomposes to methyl radicals and
nitrogen at elevated temperatures in the gas phase by a first-order process. The rate
constant depends on temperature as follows:
| T (K) |
523 |
541 |
560 |
576 |
593 |
| k (
s-1) |
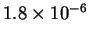 |
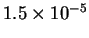 |
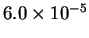 |
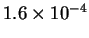 |
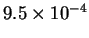 |
- (a)
- Calculate the activation energy and preexponential factor
for this reaction.
- (b)
- Calculate the entropy of activation at 550K. Based on your calculation,
comment on the nature of the transition state for this
reaction.
- 5.
- For first-order reactions in solution near room temperature,
at what approximate value of
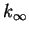 would we have
would we have
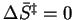 ? On a molecular level,
what is the significance of such a value of the entropy of activation?
? On a molecular level,
what is the significance of such a value of the entropy of activation?



Up: Back to the Chemistry 2710 assignment
index
Marc Roussel
2000-04-11
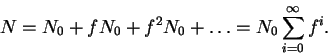
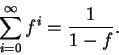
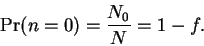
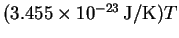 to T near 298K. How does the
equipartition value compare?
to T near 298K. How does the
equipartition value compare?
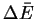 for the reaction as well as the activation
energies for the forward and reverse reactions.
for the reaction as well as the activation
energies for the forward and reverse reactions.
 ).
).