Chemistry 2710 Review Problems

1. 1. For the mechanism

      

      under what condition(s) would the equilibrium and steady-state approximations be valid?

   2. Obtain an approximate rate law using the steady-state approximation. Assuming the validity of the steady-state approximation, what would be the experimentally observed order of reaction?
   3. Suppose that 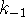is so small that it can be neglected and that 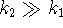. Explain what approximations can be used in this case and verify that

      

      is a solution of your approximate rate equations.  

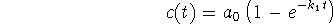
   4. Under the conditions described in question 1c, if 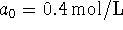and 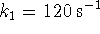, how long would it take for the concentration of product to rise to 0.2mol/L?
2. In class, we studied a version of the Lindemann mechanism in which the reactant activates itself. Of course, if there are other species in the system (e.g. inert gases like argon or nitrogen), they can also activate the reactant during collisions. Suppose that the reactant (A) pressure is low compared to the pressure of an inert gas (X). Then, collisions between A and X are much more common than collisions between two molecules of A and the Lindemann mechanism becomes

   

   Obtain an approximate rate law for this mechanism valid if is large. Discuss the dependence of the rate of reaction on the pressure of the inert gas X, paying particular attention to what happens in the limit of large or small X. Also, from the point of view of chemical realism, what problem(s) do you foresee with your rate equation is X is very small?

3. Consider the following mechanism:

   

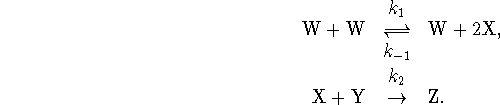
   1. What is the overall reaction? Identify the reactants, products and intermediates in the mechanism.
   2. Assuming that W is a normal molecule with fully satisfied valencies, what kind of chemical species is X?
   3. Suppose that the first step reaches equilibrium rapidly. Derive an approximate rate law valid in this case.
   4. Under what condition(s) could you apply the steady-state approximation? Derive an approximate rate law using this approximation.
4. Linearizing plots (like the Lineweaver-Burk and Eadie-Hofstee plots of enzyme kinetics) can be devised for most rate laws. Consider for instance the Lindemann mechanism. Start by showing that the rate law can be written in the form

   

   where K is a ratio of rate constants. Then show, by manipulating this equation, that a plot of a/v vs should be linear if a reaction obeys the Lindemann law. State clearly the values of the intercept and slope.

5. Consider the following mechanism for the decomposition of hydrogen peroxide in bromide solution:

   

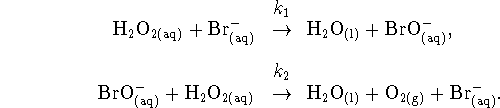
   1. What is the role of the bromide ions in this mechanism?
   2. The second step is much faster than the first. Apply an appropriate approximation to obtain the rate law for this mechanism.
6. Derive the Michaelis-Menten rate equation. Explain any assumptions or approximations used.
7. Myosin is an enzyme that catalyzes the hydrolysis of ATP, harnessing the free energy of this reaction for muscle contraction. The initial rates of this reaction are as follows:

   

   Calculate and for this enzyme/substrate system. Comment on the fit of the data to the Michaelis-Menten rate law.

8. Consider the following initial rate data for an enzyme:

   

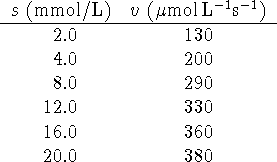
   Given that the concentration of enzyme is 2.0g/L and that its molar mass is approximately 50kg/mol, calculate and . The sum appearing in the expression for derived from the steady-state approximation ( ) is of course no smaller than . From this observation, compute a lower bound for the value of .