Chemistry 2000, Section A
Spring 1996 Test 3 Solutions

1. Denote the acid by HA.

   

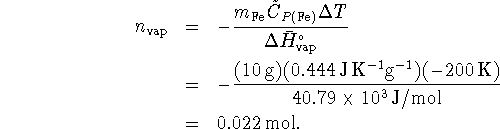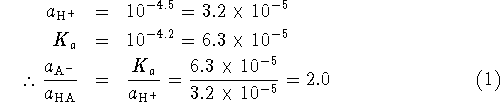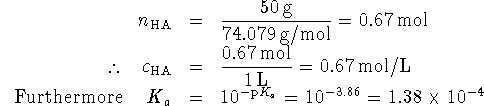
   is the equilibrium constant for the dissociation . Since is small, very little of the lactic acid will dissociate so that . Also, one proton is produced for every lactate anion so we have

   

2. We first need to convert the pH and to an activity of and to a , respectively:

    

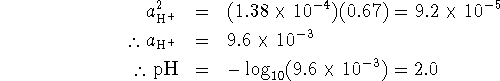
   We also want

    

   If we solve equation 1 for and substitute this result in equation 2, we get

   

3. Calcium fluoride is . is the equilibrium constant for the reaction

   

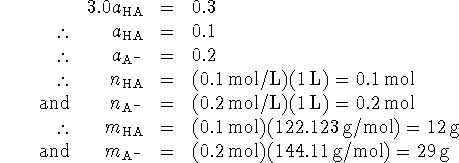
   Thus . Since two fluoride ions are liberated for every calcium ion, we have . Therefore

   

4. We first compute the initial concentration of lactose:

   

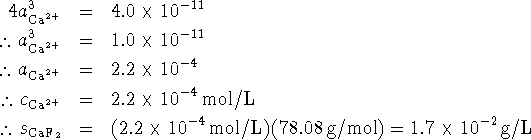
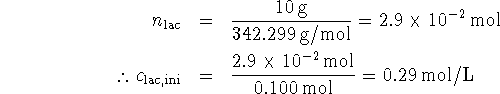
   The equilibrium constant is quite large. This implies that almost all of the lactose will have dissociated at equilibrium, leaving us with 0.29mol/L each of glucose and galactose. As for the glucose,

   

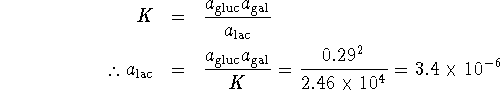
   The equilibrium concentration of lactose is therefore .

5. The water starts out at its boiling point ( ) and cannot be heated beyond this point (provided it does not superheat). The piece of iron starts out at and ends up at . The heat balance equation is therefore

   

   where is the number of moles of water vaporized. Therefore