 |
|
||||||||||||||
| Links to Notebook Pages: |
Wednesday October 25, 2006 5:25 am Lethbridge Sunrise 8:08 Sunset 18:22 Hours of daylight: 10:14
A. Morning Musings
5:25 am It is +4 C at the moment and raining. It is supposed to end later this morning and we are aiming for a high of +12.
My weight is steady at 181. That is good, particularly since the last two days were largely restaurant food.
B. Plan
Immediate Health Walk & exercise 1 hr Model Trains Assembly of CN 5930, an SD40-2 with a NAFTA logo 1 hr Mathematics Read & make notes for "Fearless Symmetry" chap 6: equations and varieties 3 hr Continue reading "The Equation that Couldn't be Solved" 2 hr Literature Continue reading "Standing Stones" by John Metcalf 2 hr Later Chores Investigate water softeners for home Technology Read manual for cell phone Make notes for chap. 4 of "Switching to the Mac" Begin reading "iPhoto" digital photography - learn about using the various manual settings
Literature Read "The Art of Living" by Epictetus Read "The Song of Roland" Mathematics Larson "Calculus" Read "The Computational Beauty of Nature" Chap 3 Gardner "The Colossal Book of Short Puzzles" History Continue reading "Citizens" Watson "Ideas" Model Trains Build oil refinery diorama: add ground cover Assemble second oil platform kit Puzzles The Orange Puzzle Cube: puzzle #9
C. Actual/Notes
8:00 am
I have read chapter 6 Equations and Varieties this morning.
There are both some genuinely new concepts for me as well as some notational conventions. This chapter may require a few re-readings before I move on.
I am reminded of a quote of Richard Feynman's where we suggested that when you read something you don't understand, go back to the beginning of the book and start over. It is good advice. The difficulty is due to a lack of understanding of something that has gone on before, but which, since you didn't 'get it" the first time, you also don't realize that you have missed it.
The first chapter is about Representations. Yet this is not a term that I can now use with comfort. Back to chapter 1.
The two major ideas so far are those of a group and those of a field.
A group is a set of elements and a binary operation (often called a composition) that describes how to obtain an element given two other elements. The set is closed under this operation (i.e. given any two elements in the set and the operation, one always obtains another element in the set). There is an identity element (usually represented by the letter e) such that for any element in the group, xe = ex = x. Every element has an inverse (i.e. xy = yx = e). Finally, the associative law holds for the operation (i.e. for any three elements, (xy)z = x(yz) ).
A field is a special type of group that has a second binary operation (the two operations are usually called addition and multiplication) where element has a multiplicative inverse. One example of a field is the set of integers 0, 1, 2, ... (p - 1) where p is a prime integer and the two operations of addition and multiplication modulo p.
Here is a concept map of the major ideas described in the first 5 chapters.
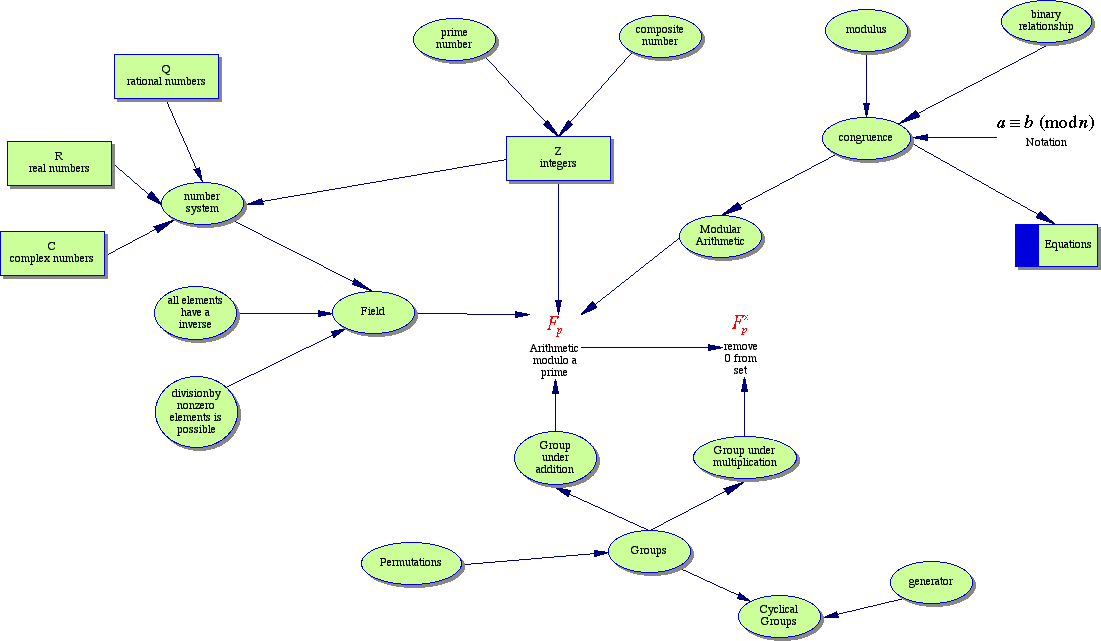
Now to make some notes for chapter 6. Making these notes also acts as a form of consolidation.
Fearless Symmetry Chapter 6 Equations and Varieties [p. 49 - 66]
- "We now come fact to face with the motivating problem of this book: equations and how to solve them." [p. 49]
- "Although ... we are primarily interested in integral or fractional solutions of systems of polynomial equations with integral coefficients ..., it will be helpful to consider also
- equations and their solutions in general, and
- solutions to equations involving number systems other than the integers." [p. 49]
- "In this chapter we broach the question: 'What are interesting structural properties of sets of solutions.' " [p. 49]
- "Many different systems of equations can define the same variety S." [p. 58]
- "Are there general methods to solve systems of polynomial equations? No." [p. 63]
- "S(A) is not just a set; it is the basis for defining a representation of a certain group, called the Galois group." [p. 66]
- Z-varieties ... leads us to the central subject of this book: Galois groups and their representations
Notations:
- Z, Q, R, C,
- S(A)
Terms
- rational number
- irrational number
- Z-equation
- variety
- roots of f(x)
- Galois groups
- elliptical curves
There were a number of new concepts and terms in this chapter: Z-equation, variety, Galois group and elliptical curves are all totally new to me. This is getting interesting!
Chapter 7 Quadratic Reciprocity [p. 67 - 83] begins by examining some special Z-equation systems and their associated varieties.
2:30 PM I have just finished reading chapters 3 & 4 of "The Equation That Couldn't be Solved". This provides a superb historical description of the state of mathematics in the 17th century and the relationship between solving equations and that of group theory. It is a nice supplement to "Fearless Symmetry" as it gives a richer sense of the setting within which the mathematical developments occurred, although it does not give much of the actual mathematics. (At least not yet.)
12:10 PM The last couple of hours have been spent fixing a leak in the pipe between the toilet bowl and the water source. I finally removed the entire fitting and went down to the hardware to see if they had something similar. They did. The way of doing things is different today than when this was originally installed but I was able to buy an entire flexible hose fitting to replace the pipe and it seems to be working. Good. Once again, it is nice to have the time for these type of home repairs.
D. Reflection


