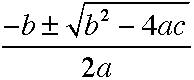|
|
||||||||||||||
| Links to Notebook Pages: |
Wednesday October 18, 2006 5:30 am Lethbridge Sunrise 7:57 Sunset 18:36 Hours of daylight: 10:39
A. Morning Musings
5:30 am It is +3 C at the moment. The forecast is for a high of + 10 C.
My weight is steady at 184.
Yesterday was spent reorganizing books in my office. By throwing away some binders containing old workshop notes as well as putting aside some books on technology that are hopelessly out of date, I was able to find room for the stacks of books that I had on the floor. This also gave me an opportunity to rearrange some of the books and to refresh my memory of what I have.
The bathroom vanity looks great. It doesn't need another coat of paint. I will remount the doors this morning, add a bumper to prevent the bathroom door from banging into the vanity, and add a toilet paper roll holder. That should take care of this project.
B. Plan
Immediate Health Walk & exercise 1 hr Chores Finish working on bathroom vanity 1 hr Model Trains Continue wiring outer mainline 1 hr Mathematics Read & make notes for "Fearless Symmetry" chap 4 3 hr Literature Complete reading "The Major Plays" by Anton Chekov 1 hr Later Chores Investigate water softeners for home Technology Read manual for cell phone Make notes for chap. 4 of "Switching to the Mac" Begin reading "iPhoto" digital photography - learn about using the various manual settings
Literature Read "The Art of Living" by Epictetus Read "The Song of Roland" Mathematics Larson "Calculus" Read "The Computational Beauty of Nature" Chap 3 Gardner "The Colossal Book of Short Puzzles" History Continue reading "Citizens" Watson "Ideas" Model Trains Build oil refinery diorama: add ground cover Assemble second oil platform kit Puzzles The Orange Puzzle Cube: puzzle #9
C. Actual/Notes
6:00 am
It has been almost a week since I made any mathematical notes. As I noted in my last session, there are two issues: understanding what one is doing, and learning how to represent this action using a specialized notation. Chapter 4 of Fearless Symmetry has more mathematics embedded in it than the previous chapters. It is easy to become overwhelmed by it.
The first step is to identify the new terms and concepts. The basic idea of modular arithmetic is one that I am familiar with. However some of the terms and even some of the notation is genuinely new to me. Great.
Fearless Symmetry Chapter 4 Modular Arithmetic [p. 31 - 41]
Notations:
- a%n
- a ∫ b (mod n)
Key People:
- Gauss
- German
- considered one of the greatest mathematicians of all time
- originated the modern notation for modular arithmetic
- Dirichlet
- German
- proved an important theorem on prime numbers, which now has his name attached to it. "An arithmetic progression contains an infinite number of primes if there is no gcd > 1 for all the numbers in the progression."
Terms
- binary relation
- congruence
- congruent modulo n
- modulus
- integer
- prime number
- composite number
- arithmetic progression
- field
- characteristic
- Euclidean algorithm
- cyclic group
- generator of a group
A good beginning.
The % notation is new to me. Apparently it is preferred by computer scientists. I wonder why. The notation means "the remainder when a is divided by n".
A slightly more complex idea is embodied in the notation developed by Gauss. a
b (mod n) means that both a and b have the same remainder when divided by n. The two numbers are said to be congruent modulo n.
Integers, prime numbers, composite numbers and arithmetic progressions are basic ideas that I have known since early undergraduate days. (I cannot recall if we met prime numbers in high school. They should be introduced in elementary school as they are one of the intriguing ideas in mathematics and it is good to let children realize that mathematics can be intriguing. The book by Conway and Guy called The Book of Numbers is another resource that is full of interesting ideas about numbers.
The mathematical concept of a field is one that I recall taking in a course on Modern Algebra, but I cannot recall anything about it. The terms characteristic, Euclidean algorithm, cyclic group and generator of a group are all new to me. It is time to engage in some new Learning.
First, for review, here are my earlier notes about groups:
- "The definition of a group is the most common way mathematicians have of formalizing the concept of symmetry. " [p. 13]
- "A group is a set along with a rule that tells how to combine any two elements in the set to get another element in the set." [p. 14]
- "We usually use the word composition to describe the act of combining two elements of the group to get a third." [p. 14]
- "The key point about a group is the combination of any two elements to get a third." [p. 15]
- "DEFINITION: A group G is a set with a composition defined on pairs of elements, as long as three axioms hold true:
1. There is a neutral element e in G, so that x o e = e o x = x no matter what element of the group is substituted for x.
2. For any element x of G, there is some element y in G so that x o y = y o x = e (y is called the inverse of x)
3. For any three elements x, y, and z in G, we have (x o y) o z = x o (y o z). (this is called the associative law)." [p. 17]
- "DEFINITION: If G is a group, the group law is the rule that tells how to combine two elements in the group to get a third. We will usually write this combination as x o y, but occasionally as x + y or even xy." [p. 18]
Now, to go on ...
- "DEFINITION: A field is a number system where we can divide by anything nonzero." [p. 36]
I find the above definition to be unhelpful. It fails (for me) to conjure up any idea or mental image of what we are talking about.
Here is the wikipedia definition of a field: http://en.wikipedia.org/wiki/Field_(mathematics).
I then returned to "Fearless Symmetry" and tried to type in a sentence involving a subscript. Here is the result:
is defined as the set {0, 1, 2, ... , p-1} with addition and multiplication defined as follows: If x, y, and z are in
, x + y = z in
exactly when x + y ∫ z (mod p) and xy = z in
exactly when xy ∫ z (mod p).
Basically, this is the pits. There must be a better way.
2:00 PM
I googled "mathematics notation Dreamweaver" and found the following web site:
The website mentions MathML (Math Markup Language) that is a new standard for creating mathematical notation within an XML environment. MathType (which I have for Windows) permits one to create web pages that use MathML or to embed a mathematics expression created in MathType (which is very easy) into a web page using MathML created in Dreamweaver. This is exactly what I want to do.
I have downloaded MathType for the Macintosh (OS X) but am having difficulty getting the embedded expression to display properly using Firefox (my web browser). I will play around a bit and see if I can get this working. At present I have a 30-day free trial, so I have time to determine if this will resolve my difficulties.
Here is an example:
This works just fine. All I am doing is creating an expression in MathType and then saving the expression as a gif file. Nothing technical about this. Let's try my previous example.
is defined as the set {0, 1, 2, ..., p - 1} with addition and multiplication defined as follows:
if x, y, and z are in
,
x + y = z in
exactly when x + y
z (mod p) and
xy = z in
exactly when xy
z (mod p).
6:05 PM A good day. The bathroom vanity if finished and I completed Anton Chekov's "The Major Plays". I returned to some mathematics Learning and we went for our hour walk even though it was cool and very windy.
D. Reflection