Saturday October 07, 2006 4:45 am Edmonton
A. Morning Musings
4:45 am It is still dark outside, not surprising given the time.
Yesterday we drove up to Edmonton, stopping off at Calgary and Red Deer on the way. A good lunch in Red Deer plus a great Chinese dinner at a restaurant in Edmonton resulted in the first time since I began keeping a record of my eating and exercise of having consumed more calories than I used. The good news is that there is no scale to weigh the effect of this for a few days. But I will have to more careful.
Another adjustment, minor but nonetheless an adjustment, is that I have no Internet access. But I do have access to my laptop.
I only brought two books with me: one on mathematics and one on history. I began both yesterday evening, but did not get too far in either. The mathematics book is "Fearless Symmetry", one that I bought in Virginia a month ago.
A few cracks are beginning to show in my approach to this web site. I am dissatisfied with the daily table that I have under section B. Plan. The immediate activities are often nothing of the kind. They should be placed in the Later section where they will not be forgotten but where it is obvious that I do not intend to act on them during the current day.
A second problem is that I am not keeping track of my various activities in terms of a "project" orientation. Related to this is a failure to keep track of potential "to do" activities as they first occur to me.
I want to devote some time this morning to mathematics and the problem of devising an appropriate format for making notes about "Fearless Symmetry". But first I want to make some coffee and then address the problems I have mentioned about this web site and time management.
I have made the adjustments to the following table. At least now the Immediate area appears more realistic. Now to try a little maths.
B. Plan
| Immediate |
|
|
| Health |
Walk & exercise |
1 hr |
| Birds |
Add September birds to North American data base |
1 hr |
| Literature |
Begin reading "Marie Antoinette " by Antonia Fraser |
1 hr |
| Mathematics |
Read & make notes for "Fearless Symmetry" chap 1 |
3 hr |
| Later |
|
|
| Chores |
Investigate water softeners for home |
|
| |
Paint new bathroom vanity cabinet |
|
| Technology |
add keywords to iPhoto records |
|
| |
Read manual for cell phone |
|
| |
Make notes for chap. 4 of "Switching to the Mac" |
|
| |
Begin reading "iPhoto" |
|
| |
digital photography - learn about using the various manual settings |
|
| Literature |
Read "The Art of Living" by Epictetus |
|
| |
Read "The Song of Roland" |
|
| Mathematics |
Larson "Calculus" |
|
| |
Read "The Computational Beauty of Nature" Chap
3 |
|
| |
Gardner "The Colossal Book of Short Puzzles" |
|
| History |
Continue reading "Citizens" |
|
| |
Watson "Ideas" |
|
| Model Trains |
Continue wiring outer mainline |
|
| |
Build oil refinery diorama: add ground cover |
|
| |
Assemble second oil platform kit |
|
| Puzzles |
The Orange Puzzle Cube: puzzle #9 |
|
C. Actual/Notes
|
Mathematics 06
October 07
|
|
Mathematics Chronology |
5:15 am
I began reading "Fearless Symmetry" yesterday evening. The book looks to be interesting, accessible, and contain a lot of mathematics that is genuinely new to me. Great!
Equally challenging is to come up with a format for making notes about this book. I lean toward some form of diagram or schematic image as a supplement to more verbal notes such as direct quotes and summary statements. The whole point of the notes is to make explicit to myself my understanding of what is being said. I want to play a bit with both Inspiration and MindManager software. |
The subtitle of the book is "Exposing the Hidden Patterns of Numbers".
Both the title and the subtitle attracted me to the book. I have always been interested in the topic of symmetry and the idea of looking for the hidden patterns of numbers was intriguing. |
Foreward [p. xv - xix] (by Barry Mazur)
- "Fearless Symmetry begins where few math books do, with an enlightening discussion of what it means for one 'thing' to represent another 'thing'. This action - deeming A a 'representation' of B - underlies much mathematics. ... What an extraordinary concept representation is and always has been. In Leibniz's essay On the Universal Science: Characteristic where he sketched his scheme for a universal language that would reduce ideas 'to a kind of alphabet of human thought,' Leibniz claimed his characters (i.e. the ciphers in his universal language) to be manipulable representations of ideas.
All that follows rationally from what is given could be found by a kind of calculus, just as arithmetical or geometrical problems are solved.
" [p. xvi]
This is not the first time I have seen reference to Leibniz's idea of a universal language for manipulating ideas, but I think it has been over 20 years. I do recall encountering the idea while I was at Queen's University.
A variation on this theme of representation might be that of diagrams. I think of Richard Feynman's diagrams for representing sub-atomic interactions as an example. I want to play with this using both Inspiration and MindManager software. The driving force is that of how to represent ideas and to show how they interact with one another. In Learning mathematics one should have as clear an idea (or complex of ideas) as one can about exactly what it is that one is doing. Unfortunately this has degenerated into the algebra of symbolic logic and proof and in the process the idea itself has become lost. This is particularly true in the case of students who are being introduced to new ideas and procedures in mathematics courses.
The issue of representation is fundamental, not only to mathematics, but also to psychology. Jerome Bruner identified this in his writings of the 1960's when he distinguished between iconic, symbolic and enactive representations. |
Preface [p. xxi - xxv]
- This book is a popular exposition of cutting-edge research in one important area of mathematics, number theory." [p. xxi]
Play time.
Let's try to capture a few ideas that seem to be central to this book:
- mathematics
- number theory
- representation
- symmetry
- idea
- concept
How can one represent these ideas?
One approach, an excellent one, is to write a paragraph or two describing what each term "means", perhaps give an example or two, and then mention some of the relationships that exist among the terms. Let's try this.
Mathematics is a branch of knowledge that is primarily about numbers and quantities and the logic of the relationships among them. There are many topics within mathematics (hundreds) although it is often difficult to make clear demarcations between these topics. One of the popular topics is that of number theory which is primarily about relationships and patterns among the integers. When one begins to discuss patterns, one then encounters the idea of symmetry which refers to a particular type of pattern. There are many different kinds of symmetry. All of this may be thought of as being embedded within the meta-branch of knowledge commonly referred to as psychology, although a good claim can be made that psychology is embedded within philosophy - particularly that branch of philosophy called epistemology.
Here is one possible representation of the ideas we have encountered so far.
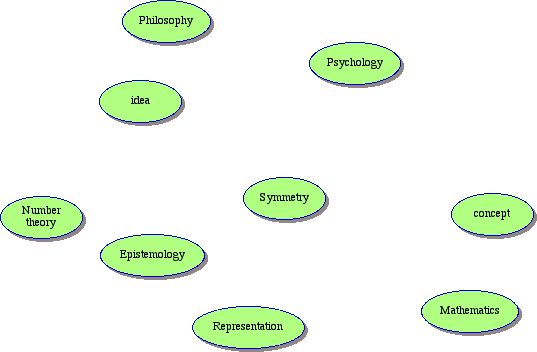
At the moment it is an amorphous jumble of ovals. For many Learners this may be a fairly good representation of their understanding at this point. There is much to commend this representation. It provides a visual image of the ideas, as well as a linguistic one. There is a fluidity implicit in the diagram. The various ovals could be placed in different locations. One may wish to try using different shapes or colors or sizes to, in some sense, improve the representation.
Here is one such image:

This latter diagram emphasizes that there are four ideas (representated by the pink "clouds", and 6 categories represented by the ovals. The large yellow cloud shows that the ideas of idea, concept and representation are important to philosophy, psychology and mathematics.
Now lets have a look at the MindManager representation.
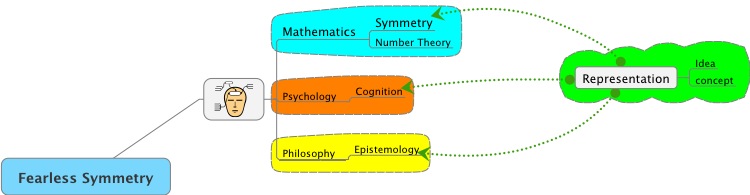
Both images show that the core ideas of representation, idea and concept are fundamental to mathematics, psychology and philosophy.
|
Chapter 1 Representations [p. 3 - 12]
- "... the basic concept of representation ... is the key concept underlying the number-theoretic methods of Galois representations that are our goal." [p. 3]
- "Say B represents A. We have three terms that stand together in some kind of relationship: A, B, and the fact that B represents A. We can call this fact X. ... Now what would be a good picture of A, B, and X?" [p. 4]
Lovely! What constitutes a "good picture"? Are the two diagrams that I produced using Inspiration and MindManager good pictures?
Frustration of a sort. Neither Inspiration nor MindManager are able to produce the simple images of a box with an arrow showing the existence of a relation between A and B.
Here is one such diagram, drawn using EazyDraw.

But this is much more trouble than it is worth. Technology sometimes falls far short of pencil and paper! The best I can do with the keyboard is x: A -> B |
- "What are representations used for? They explain one thing by means of another. The object that we want to understand is the 'thing': the thing-in-itself, the source. The object that we know quite a bit about already, to which we compare the source via a representation, we call the standard object. ... The target, the object at the head of the arrow, is the piece of the picture that we understand better. We will derive information about the source by using properties of both the arrow and the target." [p. 5]
- "DEFINITION: A set is a collection of things, which are called the elements of the set." [p. 6]
- "DEFINITION: A one-to-one correspondence from a set A to a set B is a rule that associates to each element in A exactly one element in B, in such a way that each element in B gets used exactly once, and for exactly one element in A." [p. 6]
- Counting viewed as a representation: Suppose A is a collection of things and B is the set of counting words.
In my own words: A representation is a pair of sets and a rule that describes the relation between the elements of each set. |
- "DEFINITION: A function from a set A to a set B is a rule that assigns to each element of A an element of B." [p. 9]
- "DEFINITION: A morphism is a function from A to B that captures at least part of the essential nature of the set A in its image in B." [p. 9]
- "DEFINITION: A representation is a morphism from the source object to a standard target object." [p. 10]
- "If A represents B, we have three things: two objects, A and B, which from now on will be sets, and the relation between them, which from now on will be a morphism. When A and B have some additional 'structure' - e.g. they are finite sets, or ordered sets - and we restrict the possible morphisms from A to B to have something to do with that structure - e.g. morphisms must be one-to-one correspondences, or order-preserving functions - then the existence of a representation from A to B gives us some information about A in terms of the standard object B." [p. 11]
- "In this book we will explore some very explicit examples of representations. The things we consider are always mathematical objects such as sets, groups, matrices and functions between them." [p. 11]
Let's go back to the first diagrams I created for this chapter.
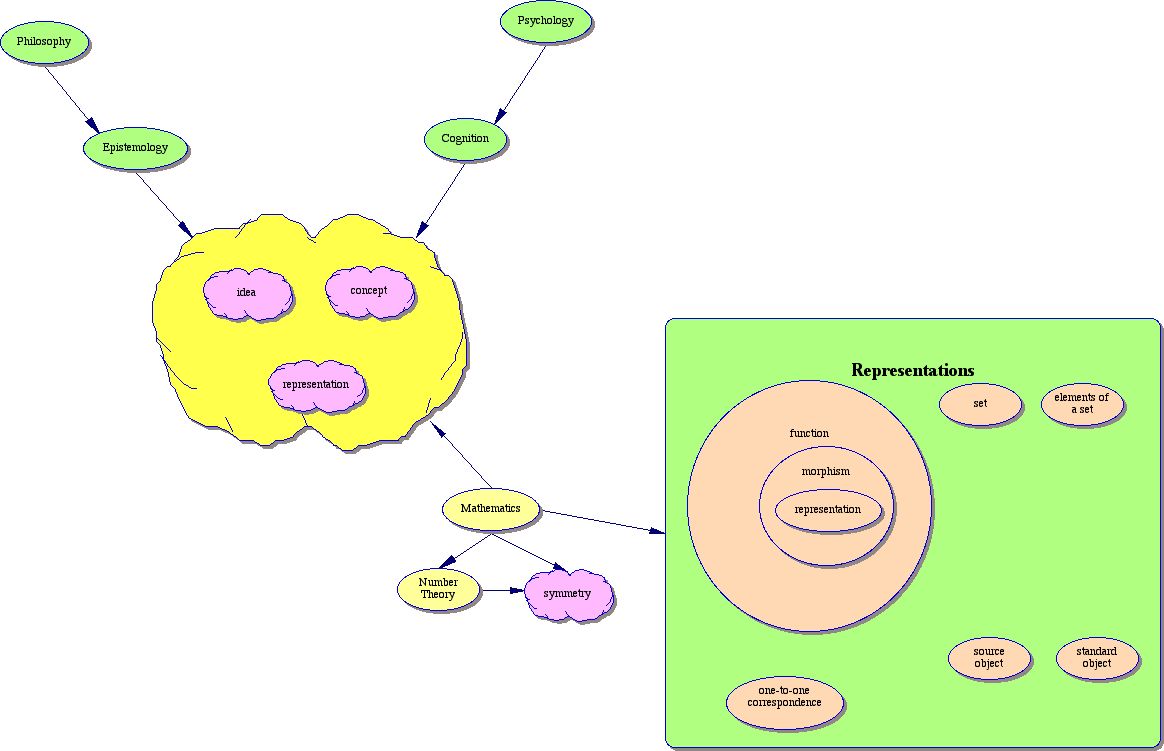
The ideas are very simple and straightforward, although the language and new terminology may appear at first sight to be convoluted and complex. A representation is a special kind of morphism which is a special kind of function. In other words, a representation is a rule that describes the relationship between two objects, usually called the source object and the standard object.
|
9:30 am A very enjoyable way to begin the day. I now have the first chapter firmly in mind.
|
9:15 PM I have brought my ToDos web page up to date. I now have 11 Learning activities identified for the month of October with 1 complete, 7 active, and 3 inactive. However I have a total of 44 other Learning activities that I have identified but have put on the back burner. It is a suggestion that I may be over-extended, but a review of the items indicates that I want to keep them on my list for a while longer.
D. Reflection |






