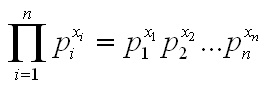Sunday August 6, 2006 6:15 am Lethbridge Alberta Sunrise 6:08 Sunset 9:06 Hours of daylight: 14:58

From rear window	South patio
Both images taken at noon

A. Morning Musings

6:30 am It is + 4 C at the moment, with a forecast high of + 27 C.

Friends are coming down from Calgary today for a visit. It will be the first time we have been together since their last visit with us while we were all in Australia in March. We are all looking forward to this.

I am having difficulty deciding on whether to use the early morning hours to tinker on the model train layout or to simply relax and read "Ada Blackjack". Or I could focus on a little mathematics. I think I will begin by making a fresh cup of coffee. ...

Done. Mmmm.

I have just measured the dimensions for the base for the oil refinery diorama. It should be 40" by 20". But I don't want to start the saw for cutting athe masonite board until after 9 am. While I am doing that I should also cut a small corner section of table top that I will need to add under some track on the reversing loop. I have made the measurements for this and will cut this board at the same time as the masonite. I also need to buy at least 2 terminal track sections, but I may as well buy a few more as I still need to think about wiring the upper layout.

B. Plan

Immediate
Health	Walk & exercise	1 hr
Mathematics	Read "The Computational Beauty of Nature" Chap 3	1 hr
Model Trains	Wire Lower Mainline Reversing loop track
	Assemble wooden trestle kit	1 hr
	Build oil refinery diorama
Literature	Begin reading "Ada Blackjack"	2 hr
Later
Chores	Investigate water softeners for home	1 hr
Technology	Read manual for cell phone	1 hr
	add keywords to iPhoto records
	Make notes for chap. 4 of "Switching to the Mac"	2 hr
	Begin reading "iPhoto"	1 hr
	digital photography - learn about using the various manual settings
Mathematics	Larson "Calculus"
	Gardner "The Colossal Book of Short Puzzles"
History	Continue reading "Citizens"
	Watson "Ideas"
Model Trains	Add blue backdrop to layout	2 hr
	Assemble second oil platform kit
	Buy some terminal track sections (2 - 6 pieces)
	Redraw diagram for Lower Mainline control panel
	Build Lower Mainline control panel
	Wire Lower Mainline turnouts

C. Actual/Notes

	Mathematics 05 August 06
Mathematics Chronology
7:40 am Chapter 3 on Computability and Incomputability has some very important, but very abstract, ideas. I recall reading about a strategy for Learning such material that was recommended by Richard Feynman. When one is no longer sure about what one is reading, go back to the beginning of the section and start over. It is a good strategy. A minor variation on this strategy is to also go back and make a new set of notes from the earlier notes. It is worth remembering that I have all of the programs that are used in the book available for use within a Windows environment. This should encourage me to play with them when they are discussed in the book. 3.1 Godelization It is possible to think of a computer program as a sequence of integers. This entire sequence of integers can be used to compute a single Godel number. And given that number, we can determine the original program. This means that we can think about computer programs and determine some of their properties by considering the properties of the corresponding Godel numbers. Thus, much of computer science can be thought of in terms of the properties of integers. The converse is also true. One can think of the properties of integers in terms of computer programs. "The key to the whole process is the fact that every number has a unique prime factorization. If you pick any natural number, x, then there is exactly one sequence of prime numbers, such that the product of the n prime numbers is equal to x. Now let's go back to looking at a program's input, which we earlier agreed to think of as a sequence of numbers. If there are n numbers in the sequence, then let every number in the sequence be denoted by x1, x2, ... , xn. To calculate the Godel number of the input string, we use the first n prime numbers and calculate which forms a unique natural number. Given a Godel number, we can reconstruct the original string by taking the prime factorization of the Godel number. If there are thirteen 2s in the prime factorization of the Godel number, then that means that the first number in the original string was 13. If there are eighty-seven 3s in the prime factorization, then the second number in the original string was 87." [p. 25] The essential idea underlying the Godel number is starting to make sense to me now. Once I have a Godel number it is relatively easy to find the prime factors of it. (either laboriously by trying each prime in order and keeping track of what still remains to be factored, or easily, by using a program like Mathematica). On the other hand, this same principle is at the heart of much of the literature on cryptography. When the numbers become very very large, then the time taken to find the prime factors may be impractically long. I suspect that is what is meant by incomputability. I shall see. ... Since every program can be represented as a string of numbers, and since every string of numbers can be represented as a single Godel number, which is also a natural number (i.e. positive integer) then it follows that the number of possible programs is the same as the number of natural numbers (which is a form of infinity). 3.2 Models of Computation A computation is a "method" for producing one number from another. A "model of computation" is a description of how one might produce such a method. One such family of models are known as general recursive functions. For example, the Successor function adds one to its argument. General recursive functions, Turing machines, and l-calculus are three well known models of computation. There are many others. Church proved, in 1941, that general recursive functions and l-calculus were equivalent. Turing later proved that Turing machines and l-calculus were equivalent, thus implying that all three models were equivalent. Any function that can be computed by these models is called computable. Every model of computation that has been considered so far has been shown to be equivalent to (or weaker than) one of these three models. 3.3 Lisp and Stutter I have realized that the different sections of the chapter provide an excellent way of compartmentalizing the topics in this chapter. I have gone back and added the section headings (in bold blue) to help make this structure explicit in my notes. Here are the remaining sections for this chapter: 3.4 Equivalence and Time Complexity 3.5 Universal Computation and Decision Problems 3.6 Incomputability 3.7 Number Sets Revisited There are many genuinely new ideas in this chapter. It is worth proceeding slowly and carefully. Lisp is a computer language created in the 1950s by John McCarthy that is based on the ideas of l-calculus and general recursive functions. Lisp is still in common use today. I think that both APL and Logo are other examples, but have not seen anything that discusses this. I have just tried googling "APL lambda calculus" and found this web site: http://en.wikipedia.org/wiki/Functional_programming. I was right! Stutter is a subset of Lisp. I have a working copy of Stutter in my Windows environment. At least for the moment I am going to ignore the details of the Stutter examples and move on to the next section. What is important for me at the moment is simply to realize that Stutter is a simple programming language that is capable of doing everything that the three models of computation are capable of. 9:00 am

 

D. Reflection