Thursday March 23, 2006 6:10 am Ballina NSW

A. Morning Musings

6:20 am The forecast is for more showers today. It is too dark at the moment to see what the sky looks like. It felt good to return to my mathematics material yesterday. I am pleased to get my three main Learning priorities clarified: Mathematics, Technology (Digital Photography) and Literature. Now to make sure that I honor them.

First, I want to copy my handwritten summary of Larson's chapter 1 onto this page. That will act as a form of slow review. Then I will have a close look at the exercises that I completed earlier for this chapter. And then I will continue the exercises. ...

Handwritten notes (made yesterday) for Larson's "Calculus", chapter 1 A Preview of Calculus:

Calculus is the mathematics of change. The key concept is that of a limit. Another important idea is that of continuity. Underlying both ideas are the concepts of function and, surprisingly, number. And intertwined among all of this is the idea of infinity. Much of the relationship between calculus, number and infinity is best discussed in courses such as analysis, functions of a real variable, functions of a complex variable and number theory.

Aside: If complex variables are the extension of number to two dimensions, what are the extensions to 3, 4, ..., k dimensions?

One should try to keep in mind at least 4 different approaches when considering a mathematics problem.

1. Numerical (tables of values)
2. Graphical (use software such as Mathematica)
3. Analytic (algebra, logic)
4. Language (use your own words).

A limit (of a function) may fail to exist for 3 main reasons:

1. The behavior of the function near the point may differ when approaching from the left and the right.
2. The function may be unbounded near the point.
3. The function may oscillate near the point.
Also, there may be complexities about the definition of the function near the point.

The Dirichlet function: f(x) = 0 if x is rational, = 1 if x is irrational, has NO limit at any real number c.

Peter Gustav Dirichlet (1805 - 1859), German, made fundamental contributions to our understanding of number.

Augustine-Louis Cauchy (1789 - 1857), French, made important contributions to calculus, including the epsilon-delta notation.

Many functions (e.g. polynomial functions, rational functions with a non-zero denominator, radical functions, and trigonometric functions) can have their limits evaluated by direct substitution. If one cannot evaluate the limit of a rational function because it has an indeterminate form (i.e. 0/0) then try either cancelling a like factor from both numerator and denominator, or by rationalizing the numerator and then cancelling a like factor.

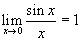
Evaluating expressions involving trigonometric functions can be very tricky because of possible indeterminate forms.

A function f is continuous at c if f(c) is defined and . End of notes.

Chores:

Mathematics: Begin working on section 1.4 of Larson's "Calculus".

Technology: Begin reading my three books on digital photography.

Literature: Continue reading "The Collected Short Stories of Roald Dahl".

C. Actual

6:20 am Begin doing some mathematics. 8:00 am

1:30 PM Mathematics. I have completed about 3 hours of working through the first few exercises for section 1.4 of Larson.

1:30 PM Now to continue reading a few short stories from "The Collected Short Stories of Roald Dahl".

Here are a few images from later this afternoon.

 

D. Reflection