9:00 am

Session 5 (Week 3a)

Chapter 2 Polynomials

Section 2.1 Exponential and Radical Expressions

1. Activities

W. Michael Kelley (2006). The Humongous Book of Calculus Problems.

Complete problems 2.1 - 2.10 [p. 16 - 18]

Wayne W. Dyer (2007). Change Your Thoughts - Change Your Life.

Read Verse 5: Living Impartially [p. 24 - 27]

2. What's it all about?

This section provides 10 problems that involve simplifying complex algebraic polynomials involving exponents (positive and negative integer, as well as fractional values).

3. What am I able to do, now that I am finished this section?

• simplify expressions involving positive integral exponents
• simplify expressions involving negative integral exponents
• simplify expressions involving square root symbols
• simplify expressions involving cube root symbols
• simplify expressions involving fractional exponents

4. What will I know?

• the rules for simplifying expressions involving exponents
• BUT I do not fully understand why these rules are the way they are (see Web for more information)

5. What are the key concepts?

• exponential notation

6. What are some relevant Web sites for this material?

Using your favorite search engine, and maybe one or two others, type in a few key words such as "exponential laws polynomials" or "exponential laws polynomials fraction ".

Here are a few Web sites that I liked:

• http://www.curriculum.org/tcf/teachers/projects/algebra/exponentlaws.adp
• http://www.mathmadesimple.com/basic-algebra/115.php
• http://www.mathmadesimple.com/basic-algebra/165.php
• http://oakroadsystems.com/math/expolaws.htm

7. What concept map can I create for this section?

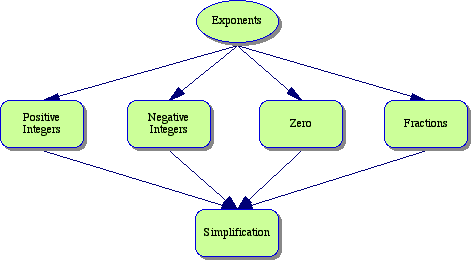
8. What types of Mathematica activities can I create?

Mathematica handles exponential and radical expressions with ease. However one must understand the notational conventions of Mathematica in order to properly express the problem initially.

9. What are some connections to other ideas?

The key idea is that of an exponent and what that means as the exponent takes on different values. This is much more subtle than the Kelley book discusses. The idea is clear when the exponent takes on positive integral values. It is simply a shorthand for repeated multiplication. But this interpretation fails to make sense when one considers values such as 0 or negative values. What does it mean to say a number is multiplied by itself -3 times?

10. What is my overall reaction to this section?

This is a very important prerequisite for calculus. Kelley notes that both differentiation and integration are closely tied to the ideas of exponents.

11. Comments on Dyer: 5. Living Impartially

This chapter makes a case for treating all individuals equally. This idea can be extended to all things, living and non-living. This is also very close to much post-modern thought. Similarly, it can be extended to the myriad of topics within mathematics. All are legitimate topics worth pursuing. Mathematics is simply a process of extending ideas in both a creative and logical manner and seeing what happens.