|
|
|
Mathematics Chronology |
7:10 am Play time. I have cut out cardboard figures for both a square and an equilateral triangle. |
Algebra: Abstract and Concrete. Edition 2.5 (online) Frederick Goodman
Chapter 1. Algebraic Themes
There are 12 sections to this chapter. The main themes appear to be symmetry (first four sections), permutations, divisibility, integers, group, rings, and fields.
1.1 What is Symmetry?
See Mathematics 12 notebook.
1.2 Symmetries of the Rectangle and the Square
See Mathematics 13 notebook.
1.3 Multiplication Tables
See Mathematics 14 notebook.
Before working on the exercises for this section I need to create a table of the positions of the vertices of the figure after each transformation.
For the square:
e |
1 2 3 4 |
no motion |
r |
4 1 2 3 |
rotate p/2 clockwise |
|
3 4 1 2 |
rotate p clockwise |
|
2 3 4 1 |
rotate 3p/2 clockwise |
a |
2 1 4 3 . |
rotate p along a axis |
b |
4 3 2 1. |
rotate p along b axis |
c |
1 4 3 2. |
rotate p along c axis |
d |
3 2 1 4. |
rotate p along d axis |
The following table means to perform the column motion first, then the row motion.
The row and column corresponding to e is easy, nothing changes. Similarly, two successive axis rotations returns the square to its original position.
Completing the rotations of r is equally straightforward, just add the exponents modulo 4.
|
e |
|
|
|
a |
b |
c |
d |
e |
e |
r |
|
|
a |
b |
c |
d |
|
r |
|
|
e |
. |
. |
. |
. |
|
|
|
e |
r |
. |
. |
. |
. |
|
|
e |
r |
|
. |
. |
. |
. |
a |
a |
. |
. |
. |
e |
. |
. |
. |
b |
b |
. |
. |
. |
. |
e |
. |
. |
c |
c |
. |
. |
. |
. |
. |
e |
. |
d |
d |
. |
. |
. |
. |
. |
. |
e |
However the remaining cells require a more careful matching of the motions with the final position of the vertices.
|
e |
|
|
|
a |
b |
c |
d |
e |
e |
r |
|
|
a |
b |
c |
d |
|
r |
|
|
e |
d |
. |
. |
. |
|
|
|
e |
r |
. |
. |
. |
. |
|
|
e |
r |
|
. |
. |
. |
. |
a |
a |
. |
. |
. |
e |
. |
. |
. |
b |
b |
. |
. |
. |
. |
e |
. |
. |
c |
c |
. |
. |
. |
. |
. |
e |
. |
d |
d |
. |
. |
. |
. |
. |
. |
e |
ar (that is, perform a motion of a and then a motion of r) gives 3 2 1 4. which is equivalent to d (using a table lookup of the transformations for the square).
The remaining cells are determined in a similar manner.
|
e |
|
|
|
a |
b |
c |
d |
e |
e |
r |
|
|
a |
b |
c |
d |
|
r |
|
|
e |
d |
c |
a |
b |
|
|
|
e |
r |
b |
a |
d |
c |
|
|
e |
r |
|
c |
d |
b |
a |
a |
a |
c |
b |
d |
e |
|
r |
|
b |
b |
d |
a |
c |
|
e |
|
r |
c |
c |
b |
d |
a |
|
r |
e |
|
d |
d |
a |
c |
b |
r |
|
|
e |
8:10 am I feel much better now that I have actually performed all of the transformations for the square. As Goodman suggests, creating a precise labeling for each of the motions is critical. So is the idea of noting which motion is performed first. A good way to begin the day. |
|
|
|
|
Mathematics Chronology |
7:30 am I will begin with exercises 1.3 |
Algebra: Abstract and Concrete. Edition 2.5 (online) Frederick Goodman
Chapter 1. Algebraic Themes
There are 12 sections to this chapter. The main themes appear to be symmetry (first four sections), permutations, divisibility, integers, group, rings, and fields.
1.1 What is Symmetry?
See Mathematics 12 notebook.
1.2 Symmetries of the Rectangle and the Square
See Mathematics 13 notebook.
1.3 Multiplication Tables
See Mathematics 13 notebook.
Exercises 1.3
1.3.1 List the symmetries of an equilateral triangle (there are six) and work out the mutiplication table for the symmetries.
Refering to Figure 1.3.6 There are 3 symmetries which involve flipping the triangle through each of its perpendicular bisectors (a, b, c) plus there are 2 rotations of 120 degrees (r and 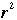 ) plus one nonmotion symmetry, e. ) plus one nonmotion symmetry, e.
|
e |
r |
|
a |
b |
c |
e |
e |
r |
|
a |
b |
c |
r |
r |
|
e |
. |
. |
. |
|
|
e |
r |
. |
. |
. |
a |
a |
. |
. |
e |
|
|
b |
b |
. |
. |
|
e |
|
c |
c |
. |
. |
|
|
e |
1.3.2 Consider the symmetries of the square card.
(a) Show that any positive power of r must be one of 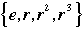 . First work out some examples, say through . First work out some examples, say through 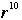 . Show that for any natural number k, . Show that for any natural number k, 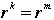 , where m is the nonnegative remainder after division of k by 4. , where m is the nonnegative remainder after division of k by 4.
(b) Observe that 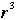 is the same symmetry as the rotation by is the same symmetry as the rotation by 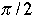 about the axis through the centroid of the faces of the square, in the clockwise sense, looking from the top of the square, that is, about the axis through the centroid of the faces of the square, in the clockwise sense, looking from the top of the square, that is, 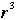 is the opposite motion to r, so is the opposite motion to r, so 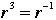 . Define . Define 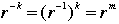 for any positive integer k. Show that for any positive integer k. Show that 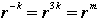 , where m is the unique element of {0, 1, 2, 3} such that m + k is divisible by 4. , where m is the unique element of {0, 1, 2, 3} such that m + k is divisible by 4.
1.3.3 Here is another way to list the symmetries of the square card that makes it easy to compute the products of symmetries quickly.
(a) Verify that the four symmetries a, b, c, and d that exchange the top and bottom faces of the card are a, ra, 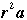 , and , and 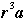 , in some order. Which is which? Thus a complete list of the symmetries is , in some order. Which is which? Thus a complete list of the symmetries is 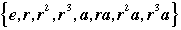 . .
(b) Verify that 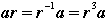 . .
(c) Conclude that 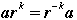 for all integers k. for all integers k.
(d) Show that these relations suffice to compute any product.
|
8:10 am Simply typing the above information has been a challenge. I have yet to actually engage in the exercises. Completing the multiplication table will be much easier after I cut out a cardboard triangle and label it. I also need to do this with a square. I am definitely at the concrete operations stage but am hopeful that a couple of hours practice with these objects will result in an improvement in my intuition.
There is a strong temptation to ignore these exercises and move on. But I am going to force myself to give this a fair go. Goodman makes a strong case for the importance of such activities. The least I can do is try. But first I need some scissors and some paper. |
|
|
|
|
Mathematics Chronology |
7:10 am Day 2 of my resolution to begin the day with some maths. I want to continue with the Goodman book on Algebra, which I enjoyed yesterday. |
Algebra: Abstract and Concrete. Edition 2.5 (online) Frederick Goodman
Chapter 1. Algebraic Themes
There are 12 sections to this chapter. The main themes appear to be symmetry (first four sections), permutations, divisibility, integers, group, rings, and fields.
1.1 What is Symmetry?
See Mathematics 12 notebook.
1.2 Symmetries of the Rectangle and the Square
Goodman points out that one could also include the motion of "no motion" (i.e. leaving the card unchanged). He claims that while this is an arbitrary choice, there are good mathematical reasons for including it.
I assume these good reasons have something to do with the idea of zero (i.e. do nothing). |
Goodman also points out that one might consider the notion that there are an infinite number of symmetries as one could continue endlessly rotating the object by multiples of the original symmetry.
I had not thought of that! But I agree that it makes sense to exclude them and focus on just those symmetries that uniquely move the object. |
Goodman then adds that he is excluding potential reflection symmetries for the moment.
I had not thought of these either. |
- "Here is an essential observation: If I leave the room and you perform two undetectable motions one after the other, I will not be able to detect the result. The result of two symmetries one after the other is also a symmetry." [p. 4]
Of course. But I had not realised this until Goodman mentioned it. It helps to have a good teacher, particularly at the early stages. |
One can consider a sequence of symmetries as a form of "multiplication". Then the product of two symmetries x and y would be written as xy where this would mean to first do y and then x.
One might also consider the sequence to a form of "addition", where x + y would mean first do y and then x. The only reason I see for prefering multiplication as the metaphor rather than addition is that it is easier to write.
I understand that it is simply a convention to say the xy means do y first. We could just as easily say xy means do x first. The issue is one of both reader and writer understanding which convention is being used. It also helps if there is a form of universal agreement as it makes the interpretation that much easier and automatic. |
- "Let's label the three nontrivial rotations of the rectangular card by
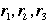 and let's call the nonmotion e. If you perform and let's call the nonmotion e. If you perform 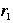 first , and then first , and then 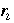 , the result must be one of , the result must be one of 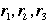 or e (because these are all of the symmetries of the card)." [p. 4 - 5] or e (because these are all of the symmetries of the card)." [p. 4 - 5]
The next task is to complete a "multiplication table" of all possible pairs of motions:
Done.
Now do the same for the square card.
|
e |
|
|
|
a |
b |
c |
d |
e |
e |
|
|
|
a |
b |
c |
d |
|
|
|
|
e |
d |
c |
a |
b |
|
|
|
e |
|
b |
a |
d |
c |
|
|
e |
|
|
c |
d |
b |
a |
a |
a |
c |
b |
d |
e |
|
|
|
b |
b |
d |
a |
c |
|
e |
|
|
c |
c |
b |
d |
a |
|
|
e |
|
d |
d |
a |
c |
b |
|
|
|
e |
8:10 am Whew! Looking at each table there are a number of patterns and regularities. |
|
|
|
|
Mathematics Chronology |
9:30 am I continue to struggle with my mathematics Learning. I am beginning to suspect that it is a form of avoidance. In my mind I have two distinct topics: calculus and abstract algebra. This latter topic is largely about group theory and symmetry. The calculus appears to be in hand. I have a good idea of the basic prerequisite of function and have a sense that the idea of limit is closely tied to the idea of number. At the same time, I am beginning to review some basic skills having to do with the manipulation of symbols. But I am struggling with the algebra. I am going to try looking at the online book by Goodman, which appears to be a good introduction using symmetry as the underlying theme.
In order to address the avoidance issue, I am going to make Mathematics my morning priority. I will try to reserve 2 hours most mornings for some maths, perhaps alternating betweeen calculus and algebra. I am not sure if I want the alternation to occur on the same day or on alternate days. I will begin with algebra this morning and see how I feel after an hour. |
Algebra: Abstract and Concrete. Edition 2.5 (online) Frederick Goodman
Chapter 1. Algebraic Themes
There are 12 sections to this chapter. The main themes appear to be symmetry (first four sections), permutations, divisibility, integers, group, rings, and fields.
1.1 What is Symmetry?
I love the opening note to the reader where Goodman shows the similarities between being a mathematician and a fly fisherman.
I also like his clear statement on the goals of the course. There are two. |
"The purpose of this course is to introduce you to the practice of mathematics; to help you learn to think things through for yourself; to teach you to see 'something noticeable which makes you see something you weren't noticing which makes you see something that isn't even visible.' And then to explain accurately what you have understood.
Not incidently, the course aims to show you some algebraic and geometric ideas that are interesting and worth thinking about." [p. xii]
Goodman goes on to say, "You must have patience, or learn patience, and you must have time." [p. xii]. I definitely have time, at least I should if I don't keep avoiding the topic. And I like to think that I have patience. To continue ... |
"We have to try to understand the integers, the rational numbers, polynomials, matrices, and so forth ..." [p. 1]
This is great. The comment is very similar to that of Spivak in his opening chapter on calculus where he notes that calculus turns out to be fundamentally about the nature of number. |
The first idea that Goodman presents is Symmetry.
Goodman suggests that the reader take some time to think about symmetry. Make a list of some symmetric objects and think about their properties.
Okay. But I just happen to have a book by David Wade (2006) which is packed with examples. |
What do I see?
The first obvious fact is the sheer number of images and examples! Symmetry is a very rich and complex topic.
The next thing I notice is that there are two basic types of example: some images are drawn and others are taken from nature.
How can one create order from all of this diversity? Wade quickly moves from two-dimensional examples to three-dimensional objects. He also moves from simple examples of translational symmetries to rotations and reflections. He also gives examples of self-similarity, radial symmetries, spherical symmetries, stacking and packing problems, left- and right-handedness, waves, spirals, helices, Fibonacci series, fractals, Penrose tilings and self-organizing systems.
I am reminded of George Polya's edict for problem solving: think of a simpler problem, or in common parlance, walk before you run. But it is nice to see that the goal is to have a better understanding and appreciation of a very rich and complex topic. That is what makes this all worth while.
I also have another book that I bought over 20 years ago, and which I have just pulled down from the bookshelf behind me. It is called "Handbook of Regular Patterns" (1980) by Peter Stevens. I have always valued this book, but have never sat down with it and tried to understand it at a deep, satisfying level. |

This fairly thick book is only about symmetry in two dimensions!
For the moment I will put this aside and continue reading the Goodman book. |
Goodman also begins with a very simple example, a rectangular sheet of blank paper and asks one to consider how many ways can one move the paper and still leave it looking the same. He then defines symmetry as follows:
Definition: A symmetry is an undetectable motion. An object is symmetric if it has symmetries.
Exercises 1.1
1.1.1 Catalog all the symmetries of a (nonsquare) rectangular card. Get a card and look at it. Turn it about. Mark its parts as you need. Write out your observations and conclusions.
Holding the card horizontally, I can rotate it 180 degrees (either clockwise or counterclockwise) and leave the card looking the same. I can also flip the card over (i.e. rotate it 180 degrees, clockwise or counterclockwise) through either of the two axes that bisect the card. Basically, that is it. There are three operations that leave the card unchanged. Therefore a rectangular card has 3 symmetries.
1.1.2 Do the same for a square card.
The three operations for a rectangular card still apply for a square card. In addition, holding the card horizontally I can rotate it 90, 180, 270 and 360 degrees and leave the card looking the same. The rotation of 360 degrees is interesting. It has the same effect as not rotating it at all. This raises the question of whether it should be counted. I can also flip the card over through either of the two axes that bisect the card (just as I could for a rectangular card). In addition I can flip the card through either of the two diagonals. Not counting the cases where the card is left in the same position, I have a total of 3 + 4 = 7 distinct symmetries.
1.1.3 Do the same for a brick (i.e. a rectangular solid with three unequal edges). Are the symmetries the same as those of a rectangular card?
I will use a book as an example of a brick. Clearly, to me, i can still perform all of the operations that I could for a rectangular card. But in addition I can also flip the brick both sidewise and lengthwise through an axis that bisects the horizontal plane of the book. The brick has 5 distinct symmetries.
|
While time consuming (about 30 minutes) this has been worthwhile. I now have a much better physical sense of the various symmetries of three very basic objects. It is easy to skip such exercises, but I trust Goodman, that such activities are crucial to the overall deep understanding of the topic. There are no shortcuts.
One must experience the concept with the body as well as with the mind. |
1.2 Symmetries of the Rectangle and the Square
Goodman points out that one could also include the motion of "no motion" (i.e. leaving the card unchanged). He claims that while this is an arbitrary choice, there are good mathematical reasons for including it.
I assume these good reasons have something to do with the idea of zero (i.e. do nothing). |
Goodman also points out that one might consider the notion that there are an infinite number of symmetries as one could continue endlessly rotating the object by multiples of the original symmetry.
I had not thought of that! But I agree that it makes sense to exclude them and focus on just those symmetries that uniquely move the object. |
Goodman then adds that he is excluding potential reflection symmetries for the moment.
I had not thought of these either. |
- "Here is an essential observation: If I leave the room and you perform two undetectable motions one after the other, I will not be able to detect the result. The result of two symmetries one after the other is also a symmetry." [p. 4]
Of course. But I had not realised this until Goodman mentioned it. It helps to have a good teacher, particularly at the early stages. |
11:20 am I have been creating these notes for almost two hours and feel like a break. The two hours simply flew by! I am looking forward to another session tomorrow. The idea of setting aside time in the morning for this activity appears to be a good one. |
|
|



