Monday March 19, 2007 5:50 am Lethbridge Sunrise 7:37 Sunset 19:41 Hours of daylight: 12:04

A. Morning Musings

5:50 am It is -5 C at the moment with a forecast high of +14 C

CBC Headline: Budget Will Target 'Fiscal Imbalance': Flaherty

The Harper government will bring down its budget today. One of the big issues will be that of the imbalance among "rich" provinces and "poorer" provinces. Since this has been a perpetual issue I will be surprised if this budget will satisfy all the provinces. We shall see.

Canadian Headline: see above

Australian Headline: (from The Australian): Santoro Affair Has Damaged Government, Howard Says

PM Howard has admitted that the recent scandal about a failure to disclose personal investments has hurt the government's popularity, but says that it will blow over by the time of the next election. We shall see.

My weight is steady at 190.

From rear window	South patio
Both images taken at noon.

B. Plan

Immediate
Mathematics	Read & make notes on chap 2 Polynomials from "The Humongous Book of Calculus Problems	1 hr
Literature	Continue reading "Baudolino" by Umberto Eco	1 hr
Technology	Convert two LPs to MP3 format	1 hr
History	Begin reading "Maya"	1 hr
Later
Technology	Read manual for cell phone
	Make notes for chap. 4 of "Switching to the Mac"
	Burn backup of images onto DVD
Mathematics	Make notes for "Mathematics: A Human Endeavor" ch 1
	Read "Fearless Symmetry" chap 9: Elliptic Curves
	Begin reading "Algebra: Abstract and Concrete" by Frederick Goodman
Model Trains	Add ground cover to oil refinery diorama
	Follow tutorial for version 8 of 3rd PlanIt
	Continue assembly of coaling tower
	Purchase DCC system
History	Read Watson "Ideas"
Philosophy	Read & make notes for "Breaking the Spell"
GO	Complete reading "Lessons in the Fundamentals of Go"
Puzzles	The Orange Puzzle Cube: puzzle #10
Major Goals
Learning	Review week's pages each Sunday
	Review all pages for the month at the end of each month
Technology	Review & edit iPhoto files for 2006
	Become proficient with cell phone
Model Trains	Become proficient with 3rd PlanIt software
	Install DCC on model train layout
GO	Learn to play GO at something better than a beginner level
Drawing	Learn to draw!! (I keep saying this, yet I have yet to put a pencil to paper).
Mathematics	Continue to play with mathematics.
Literature	Continue to read Literature
Bird Watching	Continue to engage in bird watching activities.

C. Actual/Note

6:15 am I am having my first cup. Then I meet with Frank at 8:30 for a second cup at The Ugly Mug. A fine way to begin the day and the week.

I am hoping that the four books (2 travel books on Australia, 2 bird field guides for western North America) that I ordered from amazon.ca arrive today.

The following quote is taken from the book "Algebra: Abstract and Concrete", Edition 2.5 (2006) by Frederick M. Goodman.

In mathematical practice the typical experience is to be faced by a
problem whose solution is an mystery: The fish won’t bite. Even if you
have a toolbox full of methods and rules, the problem doesn’t come labeled
with the applicable method, and the rules don’t seem to fit. There is no
other way but to think things through for yourself.
The purpose of this course is to introduce you to the practice of mathe-
matics; to help you learn to think things through for yourself; to teach you
to see “something noticeable which makes you see something you weren’t
noticing which makes you see something that isn’t even visible.” And then
to explain accurately what you have understood.
Not incidentally, the course aims to show you some algebraic and geo-
metric ideas that are interesting and important and worth thinking about.
It’s not at all easy to learn to work things out for yourself, and it’s not
at all easy to explain clearly what you have worked out. These arts have to
be learned by thoughtful practice.
You must have patience, or learn patience, and you must have time.
You can’t learn these things without getting frustrated, and you can’t learn
them in a hurry. If you can get someone else to explain how to do the
problems, you will learn something, but not patience, and not persistence,
and not vision. So rely on yourself as far as possible.

The quote is one that I totally agree with. Interestingly, it is only since I retired that I feel I have enough time. While "working", it always seemed that there were enough other activities to keep me busy that I couldn't find the time to play with mathematics. I suspect that this is also true for most students, who are taking 5 courses a semester, and who often have enough assignments, exams and other activities to keep them too busy to learn patience. The oxbridge model of few classes and more independent study with small weekly seminars would appear to be a better model. Our educational model is too structured, particularly at the undergraduate (and high school) level, for students to learn to think for themselves. We have too high a balance on teaching and not enough emphasis on learning.

	Mathematics 08 March 19
Mathematics Chronology
6:35 am I have a good hour and a half to focus on some early morning mathematics. First, I want to repeat the quote I made a few minutes ago: The following quote is taken from the book "Algebra: Abstract and Concrete", Edition 2.5 (2006) by Frederick M. Goodman. In mathematical practice the typical experience is to be faced by a problem whose solution is an mystery: The fish won’t bite. Even if you have a toolbox full of methods and rules, the problem doesn’t come labeled with the applicable method, and the rules don’t seem to fit. There is no other way but to think things through for yourself. The purpose of this course is to introduce you to the practice of mathe- matics; to help you learn to think things through for yourself; to teach you to see “something noticeable which makes you see something you weren’t noticing which makes you see something that isn’t even visible.” And then to explain accurately what you have understood. Not incidentally, the course aims to show you some algebraic and geo- metric ideas that are interesting and important and worth thinking about. It’s not at all easy to learn to work things out for yourself, and it’s not at all easy to explain clearly what you have worked out. These arts have to be learned by thoughtful practice. You must have patience, or learn patience, and you must have time. You can’t learn these things without getting frustrated, and you can’t learn them in a hurry. If you can get someone else to explain how to do the problems, you will learn something, but not patience, and not persistence, and not vision. So rely on yourself as far as possible. The quote is one that I totally agree with. Interestingly, it is only since I retired that I feel I have enough time. While "working", it always seemed that there were enough other activities to keep me busy that I couldn't find the time to play with mathematics. I suspect that this is also true for most students, who are taking 5 courses a semester, and who often have enough assignments, exams and other activities to keep them too busy to learn patience. The oxbridge model of few classes and more independent study with small weekly seminars would appear to be a better model. Our educational model is too structured, particularly at the undergraduate (and high school) level, for students to learn to think for themselves. We have too high a balance on teaching and not enough emphasis on learning. I am back to before the beginning, reviewing the material that is considered important before one begins a study of limits and calculus. This is primarily about algebra and functions. The Humongous Book of Calculus Problems (2006) by W. Michael Kelley. Chapter 2: Polynomials This book contains a series of typical problems with annotated solutions. It is easy enough to read, but a better approach is to see if one can work through the problems without looking at the annotations and then compare one's own work with that of Kelley. As I have indicated before, there are three main approaches that one might take: do the problems by hand on a sheet of paper do the problems using a word processor or web authoring system do the problems using technical software such as Mathematica. I am going to try the second approach. Section (a) Exponential and Radical Expressions 2.1 Simplify the expression This is both very easy and not so easy. I can recall the law of exponents that says that . Thus the answer is . So far, so good. But why is ? This is not so hard. means a total of a times. Therefore means which is the same as . The problem was easy, but it was worthwhile to reflect for a moment on the rationale behind the procedure. 2.1Kelley notes that the first step is to use the commutative property of multiplication to reorder the factors before invoking the law of the product of expononents.   2.2 Simplify the expression . This is simply a slightly more complex expression than the first. One also uses the law of exponents that says . Reordering the terms using the principle of commutivity, and then using the law of exponents gives 2.3 Simplify the expression . This is a nice comlication: negative exponents. A negative exponent means the same as invert and multiply. Thus 2.4 Simplify the expression . 2.5 Prove that This is a totally different kind of problem. I am not sure how to begin. Any variable raised to the zeroth power means that the variable is multiplied by itself zero times. What could that mean? The Goodman quote at the beginning of this session now has relevance! . This is the first problem that required me to think. I love it. 2.6 Simplify the expression 2.2Kelley points out that this can be further simplified by looking for factors within the square root sign that are perfect squares, and hence can be brought outside of the square root sign. Of course. 8:20 am This was enjoyable and relaxing. It was fun to get back to some basic algebra (grade 10 level of high school). Still, it takes some practice to bring back those old skills. There are no short cuts to Learning.

2:00 PM Coffee this morning was great. Lance and I traded titles of books "one must read". I then went to the local Chapter's bookstore and bought "The Tender Bar" by J. R. Moehringer. However, once in the store, the publishing gods took control, and I also bought the following:

• Of This Earth (2006) by Rudy Wiebe. This, like The Tender Bar" is a memoir of the author's growing up stories. I love Wiebe's writing and am looking forward to this.
• A Long Way Gone (2007) by Ishmael Beah. While in Mexico, I saw the author being interviewed on CNN and was impressed by the testimonial given by Jon Stewart. All three of these books are memoirs. Surprising!
• Apollo's Arrow (2007) by David Orrell. Written by a scientist/mathematician this is a non-fiction explanation of why prediction is so very difficult.
• The Dragon and the Foreign Devils (2007) by Harry G. Gelber. This is a history of China from 1100 BC to the present with an emphasis on the impact of various foreign powers (e.g. Genghis Khan, Marco Polo).
• Book of Longing (2007) by Leonard Cohen. A collection of poems. I read a few while skimming the book and was sufficiently impressed to buy the book and read them all, slowly.

But first, to continue reading Baudolino.

D. Reflection
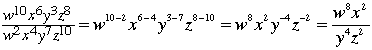
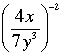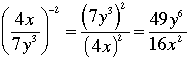
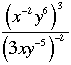