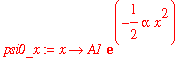
The harmonic oscillator in one and in three dimensions

Marc R. Roussel

Department of Chemistry and Biochemistry

University of Lethbridge

One dimension

I'm going to do a few calculations with the ground-state harmonic oscillator wavefunction. This wavefunction is

>	psi0_x := x -> A1*exp(-alpha*x^2/2);

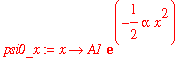
>	assume(alpha>0);

We need to normalize the wavefunction.

>	solve(int(psi0_x(x)^2,x=-infinity..infinity)=1,A1);

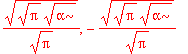
>	A1 := %[1];

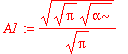
Suppose that we want to calculate the average kinetic energy. This would be

>	-hbar^2/(2*mu)*int(psi0_x(x)*diff(psi0_x(x),x$2),x=-infinity..infinity);

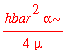
Similarly, the average of x ^2 is

>	avg_x2_1d := int(psi0_x(x)^2*x^2,x=-infinity..infinity);

It's all pretty simple in one dimension.

Three dimensions

Normalization:

>	psi0_r := r -> A3*exp(-alpha*(r-req)^2/2);

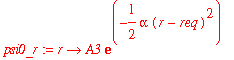
>	assume(req>0);

>	solve(int(psi0_r(r)^2,r=0..infinity)=1,A3);

>

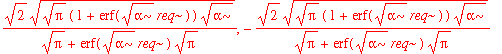
A3:=%[1];

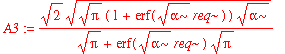
Note that the normalization factor is different  from the one-dimensional normalization factor. This isn't too surprising because in the simple one-dimensional case, we arbitrarily extend the range of integration over the entire real line. The real question is whether it makes a significant difference to our estimation of (e.g.) expectation values. Let's start with <x^2>:

>	avg_x2_3d := int(psi0_r(r)^2*(r-req)^2,r=0..infinity);

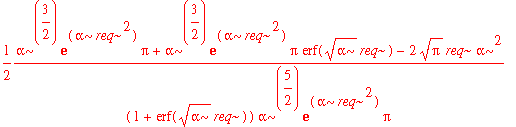
That's pretty complicated. The best way to decide whether or not this number is significantly different from the simple 1d result is by substituting in some values.

First, let's estimate alpha. The reduced mass for a diatomic molecule is typically about 10^(-26) kg (less for HX molecules). Force constants ( k ) are usually a few hundred N/m. For the sake of argument, take 200 N/m. Typical values for alpha are therefore of order

>	alpha_typical := sqrt(1e-26*200)/1e-34;

Let's estimate < x ^2> for the simple 1-d case:

>	subs(alpha=alpha_typical,avg_x2_1d);

Typical bond lengths are of order 10^(-10) m. In 3-d we therefore have

>	subs(alpha=alpha_typical,req=1e-10,avg_x2_3d);

>

evalf(%);

Hardly different at all...

Let's try it again with a high- n  wavefunction, just to make sure that there's nothing special about the low-energy states. The general formula for the 1-d harmonic oscillator wavefunctions is

>	psi_1d := (n,x) -> (alpha/Pi)^(1/4)/sqrt(2^n*n!)*exp(-alpha*x^2/2)*HermiteH(n,sqrt(alpha)*x);

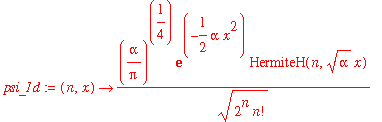
Let's check that these are normalized properly:

>	simplify(int(psi_1d(0,x)^2,x=-infinity..infinity));

>	simplify(int(psi_1d(5,x)^2,x=-infinity..infinity));

Yup.

Now let's calculate < x ^2> for (say) n =5 and n =6. (We could in principle work with higher values of n , but the integrals get hard, even for Maple, in the 3-d case.)

>	avg_x2_1d_5 := simplify(int(psi_1d(5,x)^2*x^2,x=-infinity..infinity));

>	avg_x2_1d_6 := simplify(int(psi_1d(6,x)^2*x^2,x=-infinity..infinity));

The 3-d results are going to be a little work to get because we'll have to work out the normalization constant on the fly:

>	zeta_unnorm := (n,r) -> exp(-alpha*(r-req)^2/2)*HermiteH(n,sqrt(alpha)*(r-req))/r;

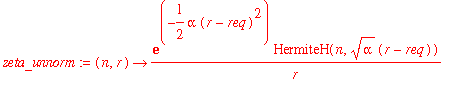
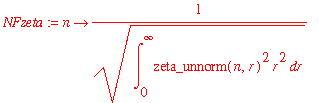
>	NFzeta := n -> 1/sqrt(int(zeta_unnorm(n,r)^2*r^2,r=0..infinity));

>	zeta := (n,r) -> NFzeta(n)*zeta_unnorm(n,r);

Verification:

>	int(zeta(0,r)^2*r^2,r=0..infinity);

>	int(zeta(5,r)^2*r^2,r=0..infinity);

We can now calculate the expectation values:

>	avg_x2_3d_5 := int(zeta(5,r)^2*(r-req)^2*r^2,r=0..infinity):

>	avg_x2_3d_6 := int(zeta(6,r)^2*(r-req)^2*r^2,r=0..infinity):

We can now do the comparison using our typical values of alpha and req:

>	subs(alpha=alpha_typical,avg_x2_1d_5);

>	evalf(subs(alpha=alpha_typical,req=1e-10,avg_x2_3d_5));

>	subs(alpha=alpha_typical,avg_x2_1d_6);

>	evalf(subs(alpha=alpha_typical,req=1e-10,avg_x2_3d_6));

The agreement is even better than for n =0!