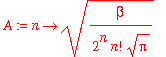
The anharmonic oscillator

Marc R. Roussel

Department of Chemistry and Biochemistry

University of Lethbridge

We start by defining the harmonic-oscillator wavefunctions, which will be the zero-order wavefunctions in our perturbation treatment of the anharmonic oscillator.

>	A := n -> sqrt(beta/(2^n*n!*sqrt(Pi)));

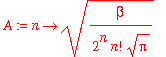
>	with(orthopoly,H):

>	psi0 := (n,x) -> A(n)*H(n,beta*x)*exp(-beta^2*x^2/2);

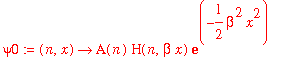
>	assume(beta>0);

The energies of the unperturbed system are given by

>	E0 := n -> (n+1/2)*hbar*omega0;

The perturbing Hamiltonian is

>	H1 := x -> 1/6*g*x^3;

The first-order correction to the ground-state energy is

>	E01 := int(psi0(0,x)*H1(x)*psi0(0,x),x=-infinity..infinity);

The even coefficients of the corrected wavefunction expressed in terms of the zero-order wavefunctions are all zero. (Why?) The odd coefficients are

>	c01 := int(psi0(1,x)*H1(x)*psi0(0,x),x=-infinity..infinity)/(E0(0)-E0(1));

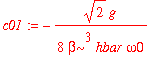
>	c03 := int(psi0(3,x)*H1(x)*psi0(0,x),x=-infinity..infinity)/(E0(0)-E0(3));

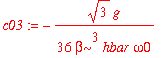
>	c05 := int(psi0(5,x)*H1(x)*psi0(0,x),x=-infinity..infinity)/(E0(0)-E0(5));

>	c07 := int(psi0(7,x)*H1(x)*psi0(0,x),x=-infinity..infinity)/(E0(0)-E0(7));

Apparently, the higher-order coefficients are all zero. This has nothing to do with any simple symmetry so is impossible to predict. However, we now have our corrected, but unnormalized wavefunction:

>	psi1_0u := x -> psi0(0,x) + c01*psi0(1,x) + c03*psi0(3,x);

To normalize this wavefunction, we look for a factor B 0 such that B 0 y  is normalized. This factor is

>	B0 := sqrt(1/simplify(int(psi1_0u(x)^2,x=-infinity..infinity)));

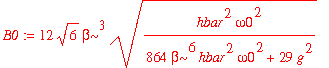
The normalized wavefunction is therefore

>	psi1_0 := x -> B0*psi1_0u(x);

We now turn to the first excited state. Only even wavefunctions will couple to it through the perturbing Hamiltonian. The coefficients are

>	c10 := int(psi0(0,x)*H1(x)*psi0(1,x),x=-infinity..infinity)/(E0(1)-E0(0));

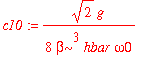
>	c12 := int(psi0(2,x)*H1(x)*psi0(1,x),x=-infinity..infinity)/(E0(1)-E0(2));

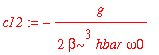
>	c14 := int(psi0(4,x)*H1(x)*psi0(1,x),x=-infinity..infinity)/(E0(1)-E0(4));

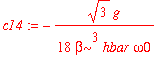
>	c16 := int(psi0(6,x)*H1(x)*psi0(1,x),x=-infinity..infinity)/(E0(1)-E0(6));

>	c18 := int(psi0(8,x)*H1(x)*psi0(1,x),x=-infinity..infinity)/(E0(1)-E0(8));

Again, it appears to be the case that the series terminates after a few terms. The unnormalized wavefunction is therefore

>	psi1_1u := x -> psi0(1,x) + c10*psi0(0,x) + c12*psi0(2,x) + c14*psi0(4,x);

We now normalize the wavefunction:

>	B1 := sqrt(1/simplify(int(psi1_1u(x)^2,x=-infinity..infinity)));

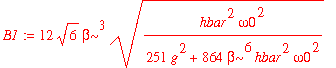
>	psi1_1 := x -> B1*psi1_1u(x);

Now suppose that we want to plot our corrected wavefunctions. We first relate b and  w 0 to k  and m :

>	assign(beta=sqrt(sqrt(k*m)/hbar));

>	omega0 := sqrt(k/m);

We now need to give values for the parameters which appear in the wavefunction. I will use SI units consistently throughout.

>	hbar := 1.1e-34;

Suppose that the particle at the end of the spring is a proton with

>	m := 1.7e-27;

We have to choose a value for k . Suppose that the proton is connected to a heavy molecule. Typical XH stretching frequencies are of the order of 5x10^{14}s^{-1}. Thus k  is typically a few hundred N/m for XH bonds.

>

k := 400;

Finally, we need to choose a value for the anharmonicity g . The anharmonicity can be computed from the dissociation energy and bond stiffness using a formula which we will see later. Realistic anharmonicities are negative. A typical value would be

>	g := -2e13;

While this seems very large, we must consider the very small amplitude of molecular vibrations in interpreting this number. The classical turning points give us an order of magnitude estimate of the vibration amplitude. Thus, the vibration amplitude is ~1/ b , i.e.

>	amp:=1/beta;

The relative sizes of the harmonic and anharmonic terms of the potential near the turning points is

>	abs(H1(amp)/(k*amp^2/2));

so the anharmonic term is relatively small, growing to 20% of the harmonic term near the classical turning points. Let us confirm this back-of-the-envelope calculation by plotting the two potentials over a reasonable range of values of x :

>	plot([k*x^2/2,k*x^2/2+H1(x)],x=-5*amp..5*amp,color=[red,blue]);

>	plot([psi0(0,x),psi1_0(x)],x=-5*amp..5*amp,color=[red,blue]);

The lower value of the anharmonic potential at positive values of x  breaks the symmetry of the wavefunction. The wavefunction "leans" to the right. A similar effect is seen in the first excited state:

>	plot([psi0(1,x),psi1_1(x)],x=-5*amp..5*amp,color=[red,blue]);

>