- (a)
- Calculate approximate energies for the ground and first
excited state of a particle experiencing the potential energy
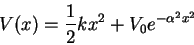
in one dimension assuming that V0 is small. [10 marks]Maple hints: eu is exp(u),
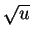 is
sqrt(u) and
is
sqrt(u) and 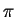 is Pi
in Maple. To use
the Hermite polynomials, enter the following into your
Maple session:
with(orthopoly,H);The Hermite polynomial Hn(u) is then accessed by H(n,u). Maple will need to know that
is Pi
in Maple. To use
the Hermite polynomials, enter the following into your
Maple session:
with(orthopoly,H);The Hermite polynomial Hn(u) is then accessed by H(n,u). Maple will need to know that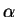 and
and 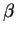 are positive parameters. Do not
define
are positive parameters. Do not
define 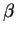 in your Maple session.
in your Maple session.
- (b)
- Sketch (qualitatively) the probability densities for the ground and first excited states of the system described in question 1a along with the corresponding densities for the harmonic oscillator. [5 marks]
Note: I know of no physical interpretation to this question.
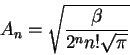
![\begin{eqnarray*}[\hat{A},\hat{A}]& = & 0\\
\mbox{}[\hat{A},\hat{B}] & = & -[\h...
...t{C}] & = & \hat{A}[\hat{B},\hat{C}]
+ [\hat{A},\hat{C}]\hat{B}
\end{eqnarray*}](img19.gif)