Up: Back to the Chemistry 2000 index
Properties of Exponential and Logarithmic Functions
- 1.
- a0=1
- 2.
-
axay = ax+y
- 3.
-
ax/ay = ax-y
- 4.
-
a-x = 1/ax
- 5.
-
(ax)y = axy
- 6.
-
![$a^{1/x} = \sqrt[\scriptstyle x]{a}$](img1.gif)
- 7.
-
(ab)x = axbx
- 8.
- Logarithms are inverse functions of exponentials:
- 9.
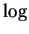 is usually a shorthand notation for
is usually a shorthand notation for 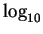 .1
I generally prefer to explicitly write down the base,
but feel free to use the shorthand if you prefer.
.1
I generally prefer to explicitly write down the base,
but feel free to use the shorthand if you prefer.
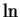 is called the ``natural logarithm''.
is called the ``natural logarithm''.
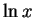 means the same thing as
means the same thing as
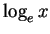 ,
where
,
where
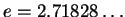 is
Napier's number. This very important logarithm comes up
in many equations in chemistry. For our purposes, you
mostly need to remember that it's just a logarithm that
behaves like all other logarithms.
is
Napier's number. This very important logarithm comes up
in many equations in chemistry. For our purposes, you
mostly need to remember that it's just a logarithm that
behaves like all other logarithms.
- 10.
-
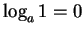
- 11.
-
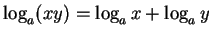
- 12.
-
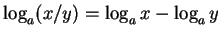
- 13.
-
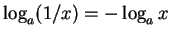
- 14.
-
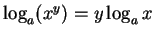
Footnotes
- ...
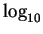 .1
.1
- One
of the reasons that I like to explicitly write down the base is
that some people, mostly mathematicians, use
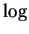 for the natural logarithm
rather than the base-10 logarithm. Writing down the base avoids
any possible confusion.
for the natural logarithm
rather than the base-10 logarithm. Writing down the base avoids
any possible confusion.
Marc Roussel
2002-01-04
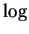 is usually a shorthand notation for
is usually a shorthand notation for 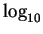 .1
I generally prefer to explicitly write down the base,
but feel free to use the shorthand if you prefer.
.1
I generally prefer to explicitly write down the base,
but feel free to use the shorthand if you prefer.
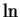 is called the ``natural logarithm''.
is called the ``natural logarithm''.
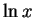 means the same thing as
means the same thing as
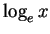 ,
where
,
where
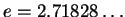 is
Napier's number. This very important logarithm comes up
in many equations in chemistry. For our purposes, you
mostly need to remember that it's just a logarithm that
behaves like all other logarithms.
is
Napier's number. This very important logarithm comes up
in many equations in chemistry. For our purposes, you
mostly need to remember that it's just a logarithm that
behaves like all other logarithms.