5:25 am Lethbridge, Alberta
I was pleased with yesterday's session. I am beginning to feel comfortable with the mathematics of number. This morning I want to have a close look at the first two chapters of Courant & Robbins
Review
Both Spivak and Courant & Robbins begin with a discussion of number. I am still struggling with finding an appropriate level of detail for studying number, before I move on to functions and limits. |
| I have skim read the first chapter of Courant & Robbins. |
Content
I am going to take the table from the previous session and try adding to it. The idea is to insert additional material from Courant & Robbins to form a more complete set of important concepts and ideas. I will try using a different color background (light blue) for this to distinguish the two sources.
The dot representation of numbers brought to mind a chapter in a small pocketbook by W. W. Sawyer called Vision in Elementary Mathematics that I have had since 1964. I want to review the first chapter on odd and even numbers using his idea of notched numbers. However beside this book on my shelf was another Sawyer classic, "Mathematician's Delight" (1943). A glance at this book shows that chapter 4 is about 'The Strategy and Tactics of Study'. I am curious to see what he says. I will make note of some of his comments in the table following the concept table. I continue to be bemused by the zig-zag nature of my activities.
Concept |
Symbol |
Description |
|
| Natural numbers |
N |
The positive integers |
3 |
| dot notation for a number |
. |
The dots may be arranged to form various shapes such as triangle, square, rectangle, notched rectangle, hexagon, ... One may then examine these shapes for patterns. |
3 |
| odd & even "dot' numbers |
. |
Use of notch to show that an odd + odd is always even |
3 |
| positional notation |
. |
Use of base 10 |
3 |
| computation in different bases |
. |
. |
2 |
| arithmetic |
. |
The mathematical theory of the Natural numbers, including the operations of addition and multiplication. |
3 |
| 5 fundamental laws of arithmetic |
. |
commutativity of addition and multiplication
associativity of addition and multiplication
distributive property of multiplication wrt addition
|
3 |
| mathematical induction |
. |
Suppose P(x) means that property P holds for the natural number x. Then P(x) is true for all x if
P(1) is true, and
whenever P(k) is true, P(k+1) is true. |
3 |
| well-ordering principle |
. |
If A is a nonnull set of natural numbers, then A has a least member.
The principle of mathematical induction may be proven from the well-ordering principle or vice-versa. |
2 |
| recursive definition |
. |
A definition that is true for n = 1 and the value for n+1 is defined in terms of n. |
3 |
| Integers |
Z |
positive and negative integers as well as zero. Z is short for the German word "Zahl", meaning number. |
2 |
| Rational numbers |
Q |
the ratio m/n of two integers, n not equal to 0. Q is short for quotient. |
3 |
| inverse operation |
. |
subtraction is the inverse operation of addition
division is the inverse operation of multiplication |
3 |
| Real numbers |
R |
numbers that can be represented by infinite non-repeating decimals. |
3 |
| prime number |
. |
a natural number having only itself and 1 as factors |
3 |
| Theorem: There are an infinite number of prime numbers. |
. |
Euclid's proof by contradiction. |
3 |
| . |
. |
There is an entire branch of mathematics devoted to theorems about prime numbers. |
1 |
| Fibonnaci sequence |
. |
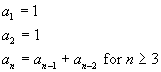
There is an entire branch of mathematics devoted to the properties of this sequence. |
1 |
Done. Now to have a close look at Courant & Robbins. |
| Here are a few quotes from "Mathematician's Delight " by W. W. Sawyer (1943) |
Quotation |
Comment |
| "The two main conditions for success in any sort of work are interest and confidence." [p. 40] |
I have these.
|
| "...the educational system seems especially designed to take all life and interest out of the subjects taught." [p. 43] |
|
| "By mathematics is meant the living subject, not what is taught in many schools." |
I have often said that there is no mathematics taught in school. I wonder if this is where I first encountered that idea. |
| "Your first job is not to learn any particular result. It is to get rid of fear. You must go back a certain way, and start with work which you are absolutely sure you can do." [p. 45] |
|
| "At some stage of the book you will find yourself again puzzled. This means that you have reached the stage where your knowledge of the subject begins to show gaps - at this point, or at some earlier point, your revision must begin." [p. 45] |
In the case of self-directed Learning, one must continually recognize this situation, and then focus on overcoming the difficulty by reviewing previous work. |
| "How long does it take to write down on a sheet of paper a list of the contents of these books, and to put a tick against the results which you thoroughly understand?" [p. 47 - 48] |
I have tried this where I use a 3-point rating scale instead of a check mark. I reinforce this with a red-yellow-green color system.
I will return to this by adding a column to the above table that uses this rating system. |
| "For anyone who wants to go on to the other branches of mathematics, meachanical learning is fatal." [p. 55] |
|
|
7:30 am
Total elapsed time: 2 hr. 5 min
Total elapsed time for the day: 2 hr. 5 min
|