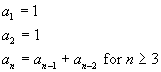Content
I have just looked up transcendental number in the MathWords web site. They are real numbers that are not algebraic (i.e. they are not the solution to a polynomial equation with integer coefficients). There is a superb diagram on this web page that shows visually that each of the following is a proper subset of those below it:
- natural numbers
- whole numbers
- integers
- rationals
- algebraic
- reals
- imaginary
- complex
Courant & Robbins begin with a chapter on the natural numbers and then add a substantial supplement on number theory. The second chapter deals with all of the other types of numbers. There are then three chapters on geometry and topology (which I think I can omit, at least for the moment), and then there is a chapter on functions and limits.
Regardless of whether I refer to Spivak or Courant & Robbins I have a substantial amount of work before I get to calculus. Fair enough!
Although the "counting numbers" (also called the Natural numbers) are familiar to everyone, it is only in the last century or so that we have developed a rigorous theoretical foundation for them. We can now state this foundation in terms of a few basic axioms and can then derive the remaining familiar properties using basic logic. The difficulty is not so much in the proofs, as it is in keeping track of exactly what has been proven so far, so one can use those theorems to prove additional theorems. For example, the familiar fact that the product of two negative numbers is a positive number is a logical consequence of these basic axioms.
We can take as a given the familiar properties of commutativity of addition and multiplication as well as the distributive property of multiplication over addition. The inverse operations of subtraction and division are easily defined as is the concept of power (exponent), although this latter concept needs elaboration in the case where the exponent is not an integer.
One new, but familiar concept is that of absolute value. The symbol for this concept is a pair of vertical lines on each side of the number. It is defined as follows:
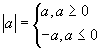
"In general, the most straightforward approach to any problem involving absolute values requires treating several cases separately, since absolute values are defined by cases to begin with." [p. 11]
I am going to create a table that captures the essential concepts of chapter 2 of Spivak:
Concept |
Symbol |
Description |
| Natural numbers |
N |
The positive integers |
| mathematical induction |
. |
Suppose P(x) means that property P holds for the natural number x. Then P(x) is true for all x if
P(1) is true, and
whenever P(k) is true, P(k+1) is true. |
| well-ordering principle |
. |
If A is a nonnull set of natural numbers, then A has a least member.
The principle of mathematical induction may be proven from the well-ordering principle or vice-versa. |
| recursive definition |
. |
A definition that is true for n = 1 and the value for n+1 is defined in terms of n. |
| Integers |
Z |
positive and negative integers as well as zero. Z is short for the German word "Zahl", meaning number. |
| Rational numbers |
Q |
the ratio m/n of two integers, n not equal to 0. Q is short for quotient. |
| Real numbers |
R |
numbers that can be represented by infinite non-repeating decimals. |
| prime number |
. |
a natural number having only itself and 1 as factors |
| Theorem: There are an infinite number of prime numbers. |
. |
Euclid's proof by contradiction. |
| . |
. |
There is an entire branch of mathematics devoted to theorems about prime numbers. |
| Fibonnaci sequence |
. |
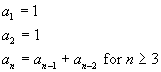
There is an entire branch of mathematics devoted to the properties of this sequence. |
Done. Now to have a close look at Courant & Robbins. |