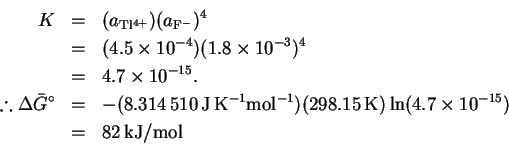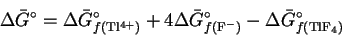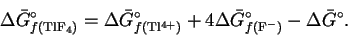Up: Back to the Chemistry 2720 test index
Chemistry 2720 Fall 2000 Test 1 Solutions
- 1.
- (a)
- The mass of water is
The heat required to warm the water to
 is
is
The heat required to vaporize the water once it reaches
the boiling point is
The total heat required is therefore
- (b)
- The process under consideration is
The equilibrium constant for this process is
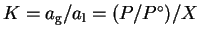 .
For pure water, X=1 so that
.
For pure water, X=1 so that
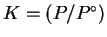 .
Therefore
.
Therefore
In our case, take
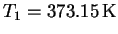 and
and
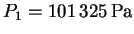 .
We want to find the boiling temperature
corresponding to the pressure
.
We want to find the boiling temperature
corresponding to the pressure
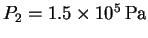 .
The enthalpy of vaporization of
water at
.
The enthalpy of vaporization of
water at
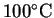 is 40.66kJ/mol.
Therefore
is 40.66kJ/mol.
Therefore
- (c)
- The pressure is constant, so the work done is
The initial volume is
The final volume is 40 times larger:
The pressure, in Pascals, is
The work is therefore
- 2.
- (a)
- The maximum work is
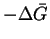 .
In this case, the
reaction only involves solids, so
.
In this case, the
reaction only involves solids, so
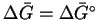 .
.
The maximum specific electrical work is therefore 4.15MJ/kg.
- (b)
- We need to find the limiting reagent:
Since we need two stoichiometric equivalents of
MnO2 per stoichiometric equivalent of zinc,
the former is clearly limiting. Accordingly,
the amount of zinc that reacts is
The maximum total work is therefore
- 3.
- (a)
- At equilibrium,
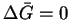 so
so
We therefore need K for the reaction
The equilibrium activity of
Tl4+ is
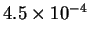 .
We get four equivalents of fluorine
for every thallium ion, so
.
We get four equivalents of fluorine
for every thallium ion, so
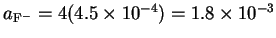 .
Thus
.
Thus
- (b)
- The free energy of reaction can be written
Rearranging, we get
Accordingly, if we can obtain values for the
standard free energies of formation of thallium
(IV) ions and of fluoride ions, we can calculate
the standard free energy of formation of
TlF4.



Up: Back to the Chemistry 2720 test index
Marc Roussel
2000-10-19
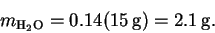
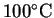 is
is
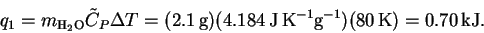
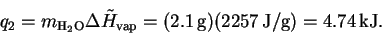
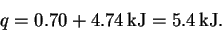
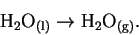
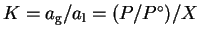 .
For pure water, X=1 so that
.
For pure water, X=1 so that
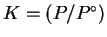 .
Therefore
.
Therefore
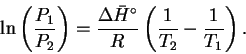
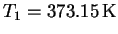 and
and
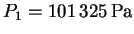 .
We want to find the boiling temperature
corresponding to the pressure
.
We want to find the boiling temperature
corresponding to the pressure
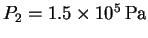 .
The enthalpy of vaporization of
water at
.
The enthalpy of vaporization of
water at
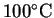 is 40.66kJ/mol.
Therefore
is 40.66kJ/mol.
Therefore
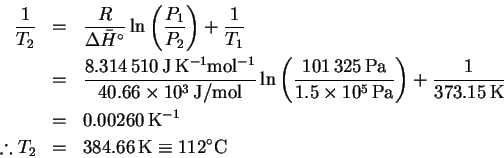
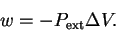
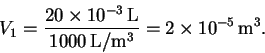
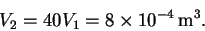
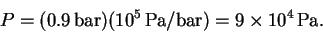
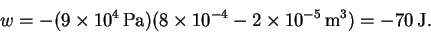
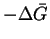 .
In this case, the
reaction only involves solids, so
.
In this case, the
reaction only involves solids, so
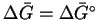 .
.
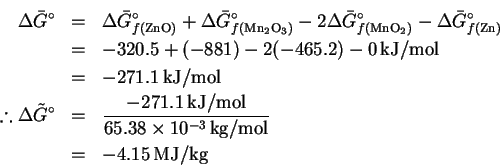

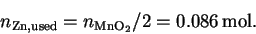
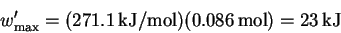
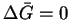 so
so
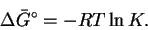
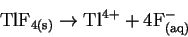
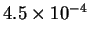 .
We get four equivalents of fluorine
for every thallium ion, so
.
We get four equivalents of fluorine
for every thallium ion, so
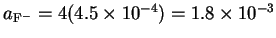 .
Thus
.
Thus