Chemistry 2720 Fall 2000 Practice Problems on Quantum Mechanics

1.

If $\ell=3$, what is the magnitude of the orbital angular momentum vector? What are the possible values of the z component of this vector? Give your answers in terms of $\hbar$.

2.

We can easily make a ``box'' for photons by making the walls out of mirrors (e.g. polished metal surfaces). Derive an equation for the energy levels of photons in a one-dimensional box of length L.

Hint: The derivation is mostly like that of ordinary particles in boxes, except that you can't use $E=\frac{1}{2}mv^2$ since photons have no mass.

3.

Cerium forms 3+ and 4+ ions. Give probable ground-state electronic configurations for the atom and its ions. Would you expect the atom and ions to be paramagnetic?

4.

Using LCAO theory, explain why mixing together p orbitals from two atoms gives both $\sigma$ and $\pi$ orbitals.

5.

Using figure 7.7 from the textbook, calculate the bond order in the molecular ion Ne₂⁺. Is this ion stable? Is it paramagnetic or diamagnetic?

6.

(a)

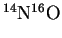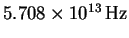The fundamental vibration frequency of $\isotope{14}{}{N}\isotope{16}{}{O}$ is $5.708\times 10^{13}\,\mathrm{Hz}$. Calculate the force constant for this molecule.

(b)

Force constants depend only on electronic effects and so are identical for isotopic variants. Estimate the fundamental vibration frequency of $\isotope{15}{}{N}\isotope{16}{}{O}$.

7.

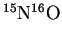(a)

Chlorophyll a absorbs photons across a range of wavelengths. The absorption maximum is at 680nm. The energy is used to fix carbon, i.e. to form carbohydrates from carbon dioxide and water. It takes about 485kJ to fix one mole of carbon. What is the minimum number of moles of 680nm photons required to fix one mole of carbon?

(b)

Experimentally, it is found that it takes 8 to 9 photons per carbon atom fixed. Quantum yield, a measure of efficiency for photochemical processes, is defined as the number of photons required divided by the actual number of photons involved in the process. What is the quantum yield for photosynthesis?

8.

(a)

The absorption rotational spectrum of the linear molecule 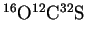$\isotope{16}{}{O}\isotope{12}{}{C}\isotope{32}{}{S}$ shows absorption lines at 24.32592, 36.48882, 48.65164 and 60.81408GHz. Calculate the moment of inertia of this molecule.

(b)

To which transition does each of the above lines correspond?

(c)

Predict the rotational Raman spectrum of this molecule if the exciting radiation has a wavelength of 336.732nm.

Isotopic masses

Isotope	Mass (amu)
$\isotope{14}{}{N}$	14.003074005
$\isotope{15}{}{N}$	15.000108898
$\isotope{16}{}{O}$	15.994914622