- (a)
- As in a hydrogen atom, the circumference must be
a multiple of de Broglie wavelength:
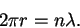
The wavelength is in turn related to the momentum by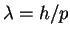 and the momentum to the speed by p=mv.
Thus we have
and the momentum to the speed by p=mv.
Thus we have
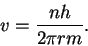
The (kinetic) energy is
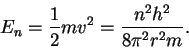
- (b)
- We need to calculate the energy of the n=3 to n=4 transition:
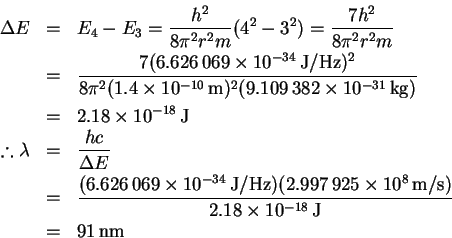
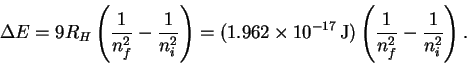
Visible lines fall (roughly) in the range 2.5-
| ni | nf | color | |
| 5 | 4 | 450 | violet |
| 7 | 5 | 517 | green |
| 8 | 5 | 415 | violet |
| 9 | 6 | 656 | yellow or orange |
| 10 | 6 | 570 | green |
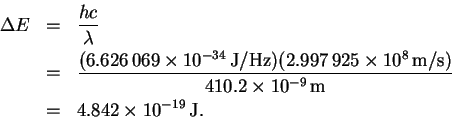
However
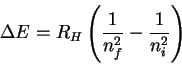
so that
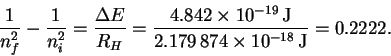
The trick now is to find a pair of values ni and nf which (at least approximately) satisfy the above relation. There is nothing for it but trial-and-error. After trying a few values, I found
Therefore the line is due to an n=6 to n=2 transition.