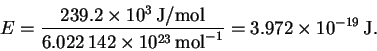
Since
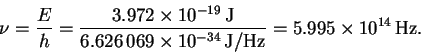
This is in the yellow-green region of the visible spectrum.
The minimum uncertainty in the position is therefore
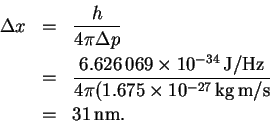
- (a)
- The wavelength is
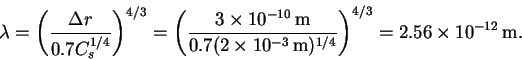
Given the wavelength, we can calculate the momentum:
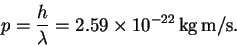
- (b)
-
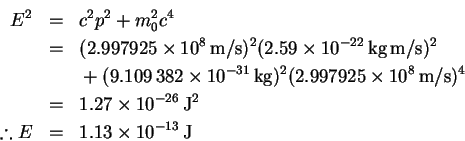
- (c)
- The kinetic energy (K) is
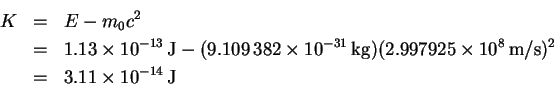
But K = eV so that
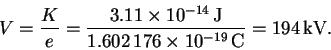
- (a)
- This is a straightforward application of the Bragg
equation
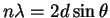 with n=1:
with n=1:
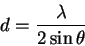
For example, the first line gives us
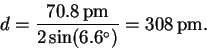
Here is a complete table of results: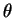 (degrees)
(degrees)6.6 9.2 11.4 13.1 14.7 d (pm) 308 221 179 156 140 - (b)
- The first reflection is probably the (100), so
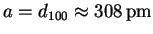 .
We then manipulate the equation for the interplane
distances:
.
We then manipulate the equation for the interplane
distances:
h2 + k2 + l2 = (a/dhkl)2.
If we were right about the first reflection being the (100) interplane distance, we should be able to determine the Miller indices corresponding to each of the other reflections by computing the approximate sum of their squares by the above formula and then finding a consistent set of indices by trial-and-error:Now that we know the Miller indices, we can calculate a = dhkl(h2+k2+l2)1/2 from each reflection and average the results.dhkl (pm) 221 179 156 140 h2+k2+l2 2 3 4 5 (hkl) (110) (111) (200) (210) The average is therefore(hkl) (100) (110) (111) (200) (210) dhkl (pm) 308 221 179 156 140 a (pm) 308 313 310 312 313 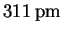 .
.
The better method is to combine the equation for the interplane distances with the Bragg condition. We get
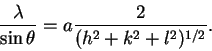
Thus, a plot of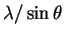 vs
2(h2+k2+l2)-1/2 should have a slope of a and an intercept near zero.
Note that the standard linear regression method
implemented in (e.g.) calculators assumes that the
abscissas are error-free while the ordinates contain
random errors so that the above-described plot is, of
all the possible ways of plotting the data, a
statistically correct choice.
The plot is reasonably linear:
vs
2(h2+k2+l2)-1/2 should have a slope of a and an intercept near zero.
Note that the standard linear regression method
implemented in (e.g.) calculators assumes that the
abscissas are error-free while the ordinates contain
random errors so that the above-described plot is, of
all the possible ways of plotting the data, a
statistically correct choice.
The plot is reasonably linear: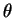 (degrees)
(degrees)6.6 9.2 11.4 13.1 14.7 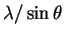 (pm)
(pm)616 443 358 312 279 (hkl) (100) (110) (111) (200) (210) 2(h2+k2+l2)-1/2 2 1.41 1.15 1 0.89 The slope is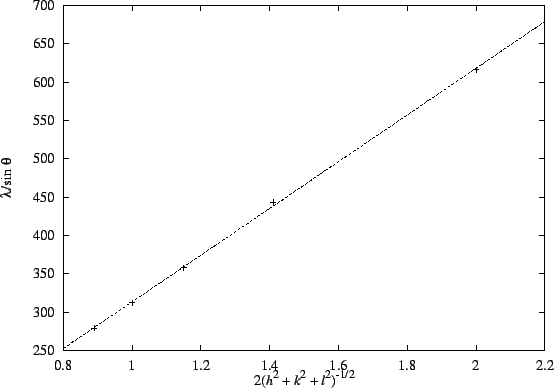
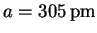 .
The intercept of
.
The intercept of
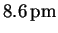 represents small systematic errors in the measurements
which slightly inflate our original estimate of a.
represents small systematic errors in the measurements
which slightly inflate our original estimate of a.