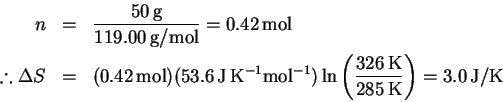- (a)
- If we add the two reactions given, we almost have
the required reaction:
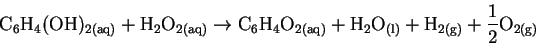
The last two terms are just water in its elemental form. If we now add in the formation reaction for water
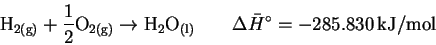
we get the desired reaction. The enthalpy change for the reaction of hydroquinone with hydrogen peroxide is therefore
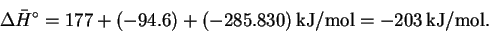
- (b)
- The density of water at
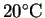 is 998g/L.
(Given the approximations being used in this problem,
the density at
is 998g/L.
(Given the approximations being used in this problem,
the density at
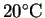 is clearly a
sufficiently close approximation to the initial density
of the solvent.)
The heat required to raise the temperature of a liter of
water from 18 to
is clearly a
sufficiently close approximation to the initial density
of the solvent.)
The heat required to raise the temperature of a liter of
water from 18 to
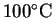 is therefore
approximately
is therefore
approximately
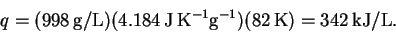
The stoichiometry of the reaction is 1:1 and the reaction generates heat in the amount of 203kJ/mol. Thus, the required concentrations of hydroquinone and of hydrogen peroxide in the compartment in which the reaction occurs are both
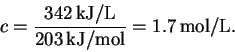
- (c)
- The change in the number of equivalents of gas is
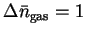 .
Thus,
.
Thus,
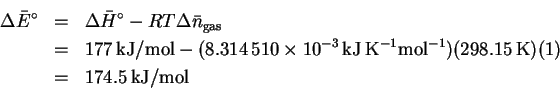
![\fbox{
\unitlength 1.00mm
\linethickness{0.8pt}
\begin{picture}
(110.00,35.00)(0...
...0){\makebox(0,0)[cc]{3}}
\put(55.00,118.00){\makebox(0,0)[cc]{2}}
\end{picture}}](img11.gif)
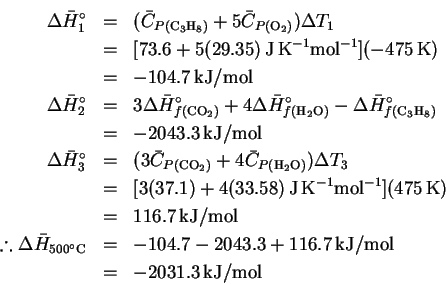
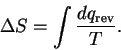
For a simple heating process, we have
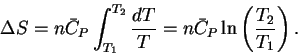
In this case,