You first have to look up the acid dissociation constant of
acetic acid. The values vary somewhat from table to table. I got
mine from Kotz and Treichel, Chemistry & Chemical
Reactivity, 3rd ed., p 808. According to this source,
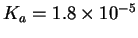 .
This is the equilibrium constant for the
reaction
.
This is the equilibrium constant for the
reaction
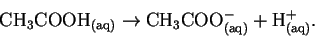
Thus
![\begin{displaymath}K_a = \frac{[\mathrm{CH_3COO^-_{(aq)}}][\mathrm{H^+_{(aq)}}]}{[\mathrm{CH_3COOH_{(aq)}}]}.\end{displaymath}](img14.gif)
There are two ways to proceed:
- (a)
- We have a total of
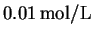 of acetic acid.
After dissociation, this means that
of acetic acid.
After dissociation, this means that
Moreover, one proton is produced for each acetate ion.
We can neglect the water equilibrium since the acid
concentration is significant and the Ka relatively
large. Accordingly,
![$[\mathrm{CH_3COO^-_{(aq)}}] \approx
[\mathrm{H^+_{(aq)}}]$](img17.gif) .
Combining these equations, we
obtain a quadratic equation. Working through this
procedure, I find
.
Combining these equations, we
obtain a quadratic equation. Working through this
procedure, I find
![$[\mathrm{H^+_{(aq)}}] = 4.15\times
10^{-4}$](img18.gif) .
I'm not showing the detailed work because
there is a simpler way which you should use whenever
possible.
.
I'm not showing the detailed work because
there is a simpler way which you should use whenever
possible.
- (b)
- The Ka is not particularly large. It follows that a
relatively small amount of acid will dissociate so that
![$[\mathrm{CH_3COOH_{(aq)}}] \approx 0.01\,\mathrm{mol/L}$](img19.gif) .
The validity of this approximation can be verified at
the end of the calculation. It is still true that
.
The validity of this approximation can be verified at
the end of the calculation. It is still true that
![$[\mathrm{CH_3COO^-_{(aq)}}] \approx
[\mathrm{H^+_{(aq)}}]$](img17.gif) .
The Ka equation becomes
.
The Ka equation becomes
Note that the answer justifies our approximations. It is
quite a bit smaller than the total amount of acetic acid
and quite a bit larger than the proton concentration
which might be obtained due to the dissociation of
water.
The difference between the answers obtained by the two
methods is negligible
on the logarithmic pH scale.
The pH is therefore 3.4.
Note that I didn't carry around units in these calculations.
There is a reason for this which we will study later in this
course.
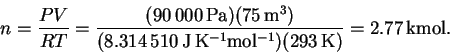
![\begin{displaymath}K = \frac{[\mathrm{C}]}{[\mathrm{A}][\mathrm{B}]}\end{displaymath}](img11.gif)
![\begin{displaymath}K_a = \frac{[\mathrm{CH_3COO^-_{(aq)}}][\mathrm{H^+_{(aq)}}]}{[\mathrm{CH_3COOH_{(aq)}}]}.\end{displaymath}](img14.gif)
![\begin{eqnarray*}% latex2html id marker 122
1.8\times 10^{-5} & \approx &
\frac...
...therefore [\mathrm{H^+_{(aq)}}] & \approx & 4.24\times 10^{-4}.
\end{eqnarray*}](img20.gif)