


Up: Back to the Chemistry 2710 assignment
index
Chemistry 2710 Spring 2000 Practice Problems: Answers and hints
- 1.
- (a)
-
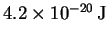
- (b)
-
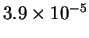
- (c)
- 99.996%
- (d)
- The CO bond is very strong (Draw a Lewis structure to see this.)
so vibrations won't contribute much to the energy. The molecule
is linear so the rotational contribution is
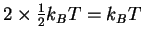 .
The translational contribution
is always
.
The translational contribution
is always
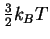 so the average total energy is
approximately
so the average total energy is
approximately
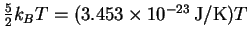 ,
which is in excellent agreement with
the equipartition value.
,
which is in excellent agreement with
the equipartition value.
- 2.
- (a)
-
- (b)
- We first need to calculate
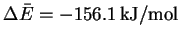 .
Then
.
Then
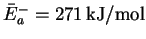 .
.
- (c)
- For the forward reaction,
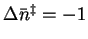 so that
so that
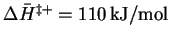 .
For the
reverse reaction,
.
For the
reverse reaction,
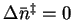 so that
so that
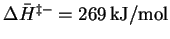 .
.
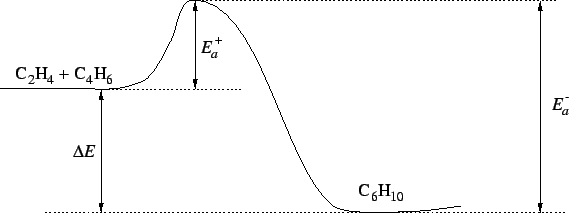
- 3.
- The reverse reaction is a radical recombination
recombination so it is all downhill. Accordingly, for the dissociation
reaction,
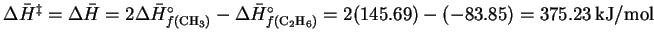 .
The transition state is not
fully dissociated so
.
The transition state is not
fully dissociated so
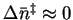 .
Therefore
.
Therefore
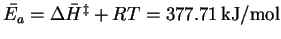 .
.
- 4.
- (a)
-
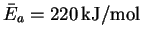 ,
,
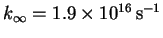 .
.
- (b)
- As an initial assumption, I'm going to guess that the
transition state is not fully dissociated, i.e. that it
is still like an azomethane molecule, only with weakened bonds.
Then
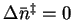 and
and
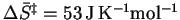 .
Since the entropy change is
positive and relatively large, there is an increase in disorder
on going to the
transition state which is probably due to a considerable
weakening of the C-N bonds. The transition state is therefore
likely more like two or three molecules than like one. We can
revise our estimate of
.
Since the entropy change is
positive and relatively large, there is an increase in disorder
on going to the
transition state which is probably due to a considerable
weakening of the C-N bonds. The transition state is therefore
likely more like two or three molecules than like one. We can
revise our estimate of
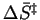 on this basis.
If we take the extreme case (
on this basis.
If we take the extreme case (
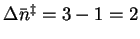 ),
we get
),
we get
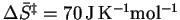 .
Reality lies somewhere between
these two extremes so we can report
.
Reality lies somewhere between
these two extremes so we can report
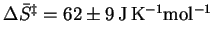 .
Whatever value we compute for
.
Whatever value we compute for
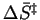 ,
we
conclude that the transition state is much more loosely bound
than the reactant, which makes good chemical sense since this
is a dissociation reaction.
,
we
conclude that the transition state is much more loosely bound
than the reactant, which makes good chemical sense since this
is a dissociation reaction.
- 5.
-
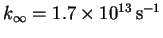 ,
assuming that room
temperature is about
,
assuming that room
temperature is about
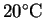 .
The condition
.
The condition
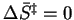 separates reactions in which the transition state is more orderly than
the reactants (negative
separates reactions in which the transition state is more orderly than
the reactants (negative
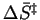 ,
,
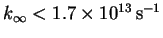 ,
corresponding to bond formation) from reactions in which the transition state
is less orderly than the reactants (positive
,
corresponding to bond formation) from reactions in which the transition state
is less orderly than the reactants (positive
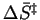 ,
,
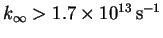 ,
corresponding to bond breaking on the way to
the transition state).
,
corresponding to bond breaking on the way to
the transition state).



Up: Back to the Chemistry 2710 assignment
index
Marc Roussel
2000-04-11
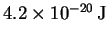
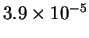
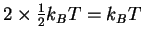 .
The translational contribution
is always
.
The translational contribution
is always
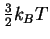 so the average total energy is
approximately
so the average total energy is
approximately
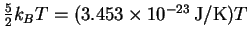 ,
which is in excellent agreement with
the equipartition value.
,
which is in excellent agreement with
the equipartition value.
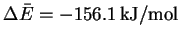 .
Then
.
Then
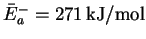 .
.
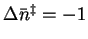 so that
so that
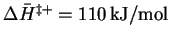 .
For the
reverse reaction,
.
For the
reverse reaction,
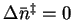 so that
so that
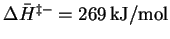 .
.
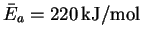 ,
,
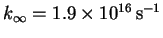 .
.
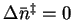 and
and
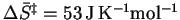 .
Since the entropy change is
positive and relatively large, there is an increase in disorder
on going to the
transition state which is probably due to a considerable
weakening of the C-N bonds. The transition state is therefore
likely more like two or three molecules than like one. We can
revise our estimate of
.
Since the entropy change is
positive and relatively large, there is an increase in disorder
on going to the
transition state which is probably due to a considerable
weakening of the C-N bonds. The transition state is therefore
likely more like two or three molecules than like one. We can
revise our estimate of
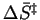 on this basis.
If we take the extreme case (
on this basis.
If we take the extreme case (
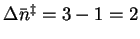 ),
we get
),
we get
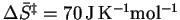 .
Reality lies somewhere between
these two extremes so we can report
.
Reality lies somewhere between
these two extremes so we can report
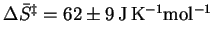 .
Whatever value we compute for
.
Whatever value we compute for
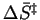 ,
we
conclude that the transition state is much more loosely bound
than the reactant, which makes good chemical sense since this
is a dissociation reaction.
,
we
conclude that the transition state is much more loosely bound
than the reactant, which makes good chemical sense since this
is a dissociation reaction.