Chemistry 2000, Section A
Spring 1996 Test 1 Solutions

1. Using the first two lines of the table, we see that the rate goes up by a factor of 5 when [A] goes up by a factor of 5. Using the last two lines, we see that the rate goes up by a factor of 4 ( ) when the [B] goes up by a factor of 2. Therefore

   

2. Different amounts of reactant disappear in 0.01s so this is not a zero-order reaction. Suppose that it's a first-order reaction. Then

   

   From the first two points, we calculate

   

   From the next two points, we get

   

   Since (within the accuracy of the data) we get the same rate constant in both cases, we conclude that this is a first-order reaction with .

3. We use the equation

   

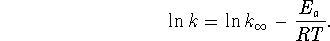
   The first experimental point tells us that

   

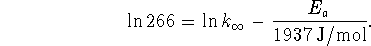
   From the second point, we have

   

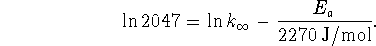
   Subtract the two equations to eliminate :

   

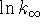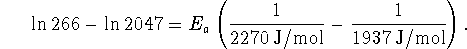
   Therefore

   

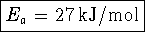
   Bonus:

   Substitute 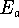into one of your two original equations and solve for :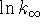

   

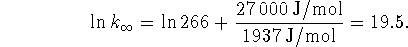
   Use 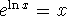to get the 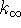out of the exponent. Recall that 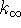has the same units as k:

   

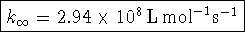
4. 1. The equations are obtained by applying the law of mass action:

      

   2. 
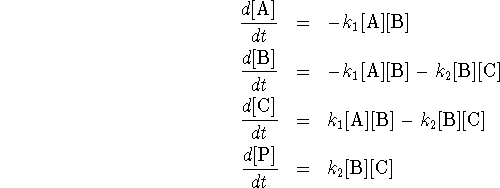
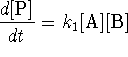
   3. Bonus: 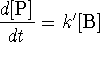where 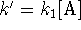is approximately constant.
5. If 99.9% of the plutonium has decayed, 0.1% of it remains. Put another way, we want to know how long it takes before . We can calculate k from the half-life:

   

   From the first-order equation, we have

   

   which is