Chemistry 2000, Fall 96, Test 1 Solutions

1. From the last two lines of the table, we see that increasing [B] has no effect on the rate. Therefore, the reaction is zero-order with respect to B so we can ignore this concentration altogether. From the first two lines, we see that doubling [A] doubles the rate so the reaction is first-order with respect to A. The rate equation is therefore

   

   The rate constant can be obtained from (say) the first line of the table using the rate law:

   

2. We want to know how long it takes before . The first-order equation can be rewritten

   

   k is computed from the half-life:

   

   

   (I believe that the true detection limits are somewhat lower so that the carbon dating method can be used to determine dates of samples somewhat older than this calculation shows.)

3. The rate equations are

   

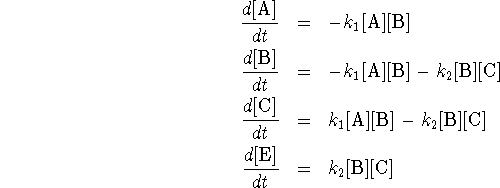
   A and B are reactants, C is an intermediate and P is a product.

4. Using the first piece of data and the Arrhenius equation, we have

   

   The second data point gives us

   

   Subtract the two equations to eliminate :

   

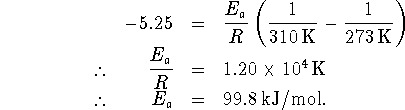
   Now substitute this data back into one of the two original equations, say the first one:

   

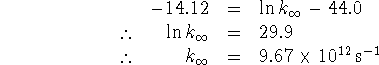
5. 1. The half-life is the time required for half the original quantity of a reactant to be removed.
   2. At 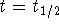, 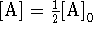. Substituting these values into the third-order equation, we have

      

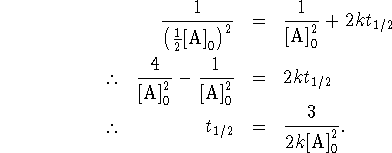
   3. The rate constant for a third-order process is in .
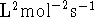   4. If we plot 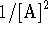as a function of time, we get a straight line of slope 2k. The rate constant is therefore extracted by dividing the slope of the plot by 2.