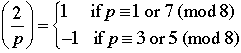Saturday November 11, 2006 6:15 am Lethbridge Sunrise 7:36 Sunset 17:54 Hours of daylight: 9:18

A. Morning Musings

6:15 am It is +1 C at the moment with a high of +7 C forecast.

From rear window	South patio
Both images taken at 11:55 am

The coffee tastes great. My weight is beginning to creep up again. Rats. My daily calorie intake is too high. Once again, the issue is portion size and snacking. It is time to reign myself in again.

Now for a few thoughts about today. I should be able to complete at least one more 100 ton quad hopper car today. I have finished one and have five more to go. I also hope to finish nailing down the track for The Channon and for the Coaldale yard. That will only leave Queenston and Pine Ridge and I will have the track finished. I will then be able to focus on completing a number of kits (primarily buildings (5) and cylindrical grain cars (4)).

I should also do some mathematics today. I would like to capture a few quotes from the book "Letters to a Young Mathematician" as well as finish the chapter in "Fearless Symmetry" on quadratic reciprocity. I think I am finally beginning to appreciate the Legendre symbol notation.

If I accomplish the above, then I may continue reading and making notes for "Citizens".

Further to the email yesterday about an upgrade to a software package called GO++, I will see if I can move the previous version that is on my PC laptop over to the Mac.

B. Plan

Immediate
Health	Walk & exercise	1 hr
Model Trains	Continue assembly of 6 quad hopper cars	1 hr
	Complete nailing track for The Channon	1 hr
Mathematics	Read & make notes for "Fearless Symmetry" chap 7: quadratic reciprocity	1 hr
	Make notes for "Letters to a Young Mathematician"	1 hr
History	Continue reading & making notes for "Citizens"	2 hr
Technology	Move GO++ software from PC to Mac	1 hr
GO	Begin playing GO++ on a 9x9 board	1 hr
Literature	Begin reading "Empire of the Sun" by J. G. Ballard	1 hr
Later
Chores	Investigate water softeners for home
Technology	Read manual for cell phone
	Make notes for chap. 4 of "Switching to the Mac"
	Begin reading "iPhoto"
	digital photography - learn about using the various manual settings
Philosophy	Read "The Art of Living" by Epictetus
Mathematics	Larson "Calculus"
	Read "The Computational Beauty of Nature" Chap 3
	Gardner "The Colossal Book of Short Puzzles"
History	Watson "Ideas"
Model Trains	Build oil refinery diorama: add ground cover
	Assemble second oil platform kit
	Assembly of CN 5930, an SD40-2 with a NAFTA logo
Puzzles	The Orange Puzzle Cube: puzzle #9

C. Actual/Notes

8:40 am I have successfully moved my copy of GO++ (version 5) over to the Mac. I was not able to install the program as a program as it wanted the source to be on a CD rather than as a folder on the desktop. Another weakness of windows xp. However the program executes just fine from the folder on the desktop so I am operational. I played a couple of 9x9 games, setting the computer to "weak", and won. This is a game that I must begin playing again. Given my level of expertise (lousy) I do not see a need to buy the new version 7. I am not sure if I want to begin making Notes about my Learning for this activity. Like mathematics, this is a topic where the Learning is genuinely new, and as such it provides a setting for monitoring self-directed Learning. I will mull this over before committing to a course of action.

	Mathematics 18 November 11
Mathematics Chronology
9:00 am I read Ian Stewart's small book "Letters to a Young Mathematician" (2006) a couple of days ago and would like to capture a few of the sentences. Letters to a Young Mathematician (2006). Ian Stewart. "A typical day for the modern academic is ten or twelve hours long, with teaching commitments, research grants to pursue, research to be carried out, and liberal doses of pointless bureaucracy to get in the way of anything creative." [p. x] "Our society consumes an awful lot of math, but it all happens behind the scenes. The reason is straightforward: that's where it belongs." [p. 2] "So each conversation is broken up into thousand upon thousands of short pieces, and only one piece in a hundred is actually transmitted. At the other end, the missing ninety-nine pieces are restored by filling in the gaps as smoothly as possible." [p. 5] Fascinating. I didn't realize that we didn't send all of the packets. I thought I was reading a math book and I end up Learning more about the Internet. "What math does for me is this: It makes me aware of the world I inhabit in an entirely new say. It opens my eyes to nature's laws and patterns. It offers an entirely new experience of beauty." [p. 7] "Some people think that this kind of understanding 'spoils' the emotional experience. I think this is rubbish. It demonstrates a depressing sort of aesthetic complacency. ... they suffer from a serious lack of curiousity: they refuse to believe the world is more wonderful than their own limited imaginations." [p. 8] "When I look at a crystal, I am aware of the beauties of its atomic lattice as well as the charm of its colors." [p. 9] "Then there's the inner beauty of mathematics, which should not be underrated. Math done 'for its own sake' can be exquisitely beautiful and elegant." [p. 9] "So he spent all of his free periods teaching us extra math, outside of the syllabus. During the regular math lessons he told us to sit at the back and do our homework; not just math, any homework. And to shut up. Those lessons weren't for us; we had to give the others a chance." [p. 14] "An awful lot of what is now called 'mathematics' at school is really arithmetic. ... 'Modern' is a strange word to use here: it means between one and two hundred years old, as opposed to the two-hundred years old math that formed the bulk of the older syllabus." [p. 19] "At university you will encounter a much broader conception of mathematics. ... You may learn how the great mathematicians of the Renaissance solved cubic and quartic equations ... if so, you will probably find out why such methods fail for quintic equations. You will see why this becomes almost obvious if you ignore the numerical values of the equations' solutions and instead think about their symmetries, and why it is arguably more important to understand the symmetries of equations thatn to be able to solve them." [p. 20] This is exactly what I am reading about at the moment in both "The Equation That Couldn't Be Solved" and in "Fearless Symmetry". "... you will find that you can recognize mathematics when you see it, but you still can't define it. Which is as it should be. Definitions pin thing s down, they limit the prospects for creativity and diversity. ... Math, like anything still under development, always has the potential to surprise." [p. 22] "Our brains are not like computers, working systematically and logically. They are metaphor machines that leap to creative conclusions and belatedly shore them up with logical narratives." [p. 23] "Or, as my friend David Tall often says, 'Math is not a spectator sport.' " [p. 24] "Math is not a robotic way of replacing thought by rigid ritual. It is the most creative activity on the planet." [p. 33] "Why do so many people think that their school textbook contains every possible question?" [p. 34] Locate "To Talk of Many Things" by Dame Kathleen Ollerenshaw. [p. 35] "... the texts do not ask questions that the methods being taught cannot answer. So, isidiously, we absorb the lesson that every mathematical question has an answer. It's not true." [p. 37] "When you study any subject, the rate at which you can understand new material tends to accelerate the more you already know." [p. 39] "... pretty much everything that students are exposed to boils down to buttons you could push on a pocket calculator." [p. 40] "Questions ... are important because our efforts to find the answer reveal major gaps in our understanding of mathematics." [p. 43] "But math is not about sums, not really. It's about patterns ad why they occur. Nature's patterns are both beautiful and inexhaustible." [p. 46] "... ideas in mathematics seem to arise in three stages: ... preparation ... incubation followed by illumination ... verification." [p. 54 - 55] "You need to understand how to learn." [p. 63] "Many students believe that if you get stuck, you should stop. ... I always tell my students that the first thing to do is read on. ... Often the next sentence, or the next paragraph, will resolve your problem." [p. 64] "If you are still stuck ... now is the time to ... ask for assistance." [p. 65] "Whenever you get stuck on a piece of mathematics, it usually happens because you do not properly understand some other piece of mathematics, which is being used without explicit mention on the assumption that you can handle it easily." [p. 65] "Read around your subject. Do not read only the assigned text. ... Find some books on the same topic or similar topics. Read them, but in a fairly casual way." [p. 67] "Microscopes made biology more interesting, not less, by opening up new ways to approach the subject. It's the same with computers and mathematics." [p. 82] "Computer-assisted proofs raise issues of taste, creativity, technique, and philosophy." [p. 106] "It's fine for people to advocate their point of view on how math should be done. But they should not presume that there is only one good way to do math. I prefer diversity." [p. 140] "You should use the tools at hand, adapt and modify them to suit your own projects, and make new ones as the need arises." [p. 146] "I read a lot, often in fields unrelated to my own, and my best ideas often come when something I have read reminds me of something I already know about." [p. 153] This describes me to a T. "We now have a highly prescriprive 'national curriculum', and teachers - quite literally - check hundreds of boxes to mark the student's progress. ... The assumption is that what really matters is their ability to get the answer. But what really matters is how they get the answer. ... I am absolutely certain that checking a series of boxes is not the way to teach anyone mathemtics." [p. 167] 2:40 PM Now to return to "Fearless Symmetry" and quadratic reciprocity. The authors make a special point of highlighting the importance of a good notation and how that may guide thinking. They mention the Legendre symbol as a case in point. Here is the notation: What does it mean? At least in the present context it refers to a pattern related to solutions to the equation . This quadratic equation will have either 0, 1 or 2 solutions depending on the values of a and p. The Legendre symbol gives the values of -1, 0 or 1 depending on the number of solutions. Amazingly, this function has a number of interesting properties. 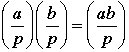For example: Theorem 7.2 Let a be a positive integer. 1. If p and q are two odd primes so that , then . 2. If p and q are two odd primes so that , then . It turns out that this is difficult to prove, but we can use the result and continue. Theorem 7.3 (Quadratic Reciprocity) Suppose that p and q are odd primes. 1. 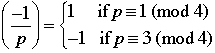2. 3. If . 4. If p or q or both are . Why do we care about all of this? Because we can use these results to compute Legendre symbols for large numbers by using the known values for much smaller numbers and this is a way of knowing whether certain quadratic equations have 0, 1 or 2 solutions, without actually having to find the solutions. From a practical point of view one may view this as an improvement, or maybe not (who cares about quadratic equations anyway). Alternatively, there is something very beautiful and magical about being to do this. Now it is possible to know if certain quadratic equations have a solution without actually having to find it. From the point of view of logic this is indeed very cool. 3:30 PM

1:30 PM On our way back from our walk we spotted a few Pine Grosbeaks in a tree overlooking the path. The male was a beautiful dark crimson head and breast. This was not a lifer, but it was a new bird for this year (#72).

D. Reflection