|
Mathematics 22
November 20
|
|
Mathematics Chronology |
5:30 am
I am not satisfied with my note making yesterday about abstract algebra. The main problem is with the proofs. I do not fully understand the logic nor the sequence of steps in them yet. I am like a dog worrying a bone. I want to feel fully in control of this. I have four books on the topic, one an undergraduate text, the other three at either an upper-level undergraduate or a graduate level.
Surprisingly, I feel that the first chapter of Michael Spivak's textbook "Calculus" to provide the best introduction to the basic properties of numbers.
Spivak provides a meticulous sequence of steps to show that if x + 3 = 5, then x = 2. He then goes on to say, "Naturally, such elaborate solutions are of interest only until you become convinced that they can always be supplied. In practice, it is usually just a waste of time to solve an equation by indicating the steps so explicitly..." [p. 5]
Now to make some notes on "Contemporary Abstract Algebra" Second edition. by Joseph Gallian (1990). |
Chapter 0 Preliminaries
- Properties of Integers
- Modular Arithmetic
- Mathematical Induction
- Equivalence Relations
- Functions (Mappings)
- Exercises
Properties of Integers [3 - 7]
Well Ordering Principle. Every nonempty set of positive integers contains a smallest member.
This is self-evident. Think of any set of positive integers. For example {3,12, 2, 99}. Reorder the numbers from smallest to largest. Then the first number in the reordered set will be the smallest member. In this example, the reorderd set is {2, 3, 12, 99} and the smallest member is 2.
The principle also applies to any finite set of integers, positive, negative or zero, but it does not apply to the infinite set of all integers since there is no end to the number of negative integers and thus this set does not have a smallest number.
Definition: A nonzero integer t is a divisor of an integer s if there is an integer u such that s = tu.
Notation: In this case we write t | s and say "t divides s"
Definition: A prime is a positive integer greater than 1 whose only positive divisors are 1 and itself.
Theorem: Division Algorithm
Let a and b be integers with b > 0. Then there exist integers q and r with the property that a = bq + r where 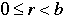 . .
Definition: q is called the quotient upon dividing a by b, and r is called the remainder.
Examples: Suppose a = 28 and b = 3. Then 28 = 9x3 + 1. That is, when 28 is divided by 3 the quotient is 9 and the remainder is 1. But one must be careful. Suppose a = -28 and b = 3. Then -28 = (-10)x3 +2. The quotient is -10 and the remainder is 2.
Definition: The greatest common divisor of two nonzero numbers a and b is the largest of all the common divisors of a and b.
Notation: gcd(a, b)
Definition: When gcd(a, b) = 1, we say a and b are relatively prime.
Theorem: GCD is a Linear Combination
For any nonzero integers a and b, there exist integers s and t such that gcd(a, b) = as + bt.
Theorem: Euclidean Algorithm (Rotman, p. 5)
Let a and b be positive integers. There is an algorithm that finds the gcd, d, and there is an algorithm that finds a pair of integers s and t with d = sa + tb.
The algorithm iterates the division algorithm. Begin with b = qa + r, where 0 <= r <=a.
Example: Suppose a = 2520 and b = 154.
2520 = 154x16 + 56
154 = 56x2 + 42
56 = 42x1 + 14
42 = 14x3
Therefore gcd(2520, 154) = 14.
| This is a real improvement over yesterday's notes. But I do not yet feel that the above has been totally integrated into my understanding of what I am doing. Time for a break, but I want to return to this. 7:10 am |
|
|
Mathematics 21
November 19
|
|
Mathematics Chronology |
6:10 am
I am having a first look at Joseph Rotman's (2002) "Advanced Modern Algebra". |
Chapter 1 Things Past
- 1.1 Some Number Theory
- 1.2 Roots of Unity
- 1.3 Some Set Theory
This is my first experience with a graduate level textbook on modern algebra.
My first thought is to see if I can come up with a visual representation of the material using either MindManager or Inspiration software. Since I will be using considerable mathematical notation, I will have to use MathType to create the expressions and then see if I can import these into the appropriate diagrams.
The book begins with a number of definitions, axioms, propositions, theorems and corollaries. The challenge is to see if I can create a map that shows the relationships among these various entitities. The propositions, theorems and corollaries all require a proof. I will begin by ignoring the actual proofs and see if I can simply see the pattern of what has been developed. |
Here is a skeleton structure using Mindmanager:

I like using color, and to a lesser extent, shape, to identify the different types of information. This is a no-nonsense book. It is simply a list of important definitions, propositions, and theorems. In this chapter, which is considered to be a review, many of the proofs are just sketched out rather than rigorously proven.
One important issue it the relative importance of these proofs. Is that what Number Theory is really all about: a structure of rigorous definitions and proofs? Or is most of the topic understanding what the various theorems say and then moving on, until one arrives at an area that is close to original research?
My sense at the moment is that it is a little of both. It is probably a good idea to study some of the proofs for the more important theorems, and to skim over much of the rest.
Another issue is this way of making notes. The backbone software is Dreamweaver, which I am using to create these web pages. When should I switch to MindManager and work within that environment. In both cases I also need to use MathType to create mathematical expressions, and in both cases I can copy and paste images and text from MathType into Dreamweaver or MindManager.
I am going to stay with MindManager for a bit and see how that goes...
I recall using a table format within Dreamweaver as a template for proofs. Let's see if I can find a previous example. I recall that it was while studying the Spivak book on calculus. Nope. I couldn't seem to find a page that matched the template in my mind. An indication that my web site still needs some refinement.
Let me try rewriting the proof for Proposition 1.1 using a table format. |
Proposition 1.1 Every integer n > 1 is either a prime or a product of primes.
Proof:
| Step |
Description |
Reason |
1 |
Let C be the subset of N consisting of all those n > 1 for which the proposition is false. That is, C contains numbers that are not prime and not a product of primes. |
The goal is to show that C is the empty set. |
2 |
Assume C is nonempty. |
|
3 |
Then C contains a smallest integer, say, m. That is, m is a member of C. |
Least Integer Axiom |
4 |
Suppose m is not a prime |
|
5 |
Then m is not a product of primes. |
step 1 + step 4 |
6 |
Therefore there are natural numbers a and b with m = ab, a < m, and b < m |
|
7 |
Neither a nor b lies in C |
Both a and b are less than m, which is the smallest integer in C |
8 |
Therefore a and b are each either prime or a product of primes. |
|
9 |
Therefore m = ab is a product of (at least) two primes. |
Contradicts step 5 |
|
Therefore C is the empty set. |
|
2:20 PM I am back from the uni library with 3 books on abstract algebra:
- Abraham P. Hillman & Gerald L. Alexanderson. Abstract Algebra: A First Undergraduate Course. (1994). Fifth Edition.
- Robert B. Ash. (1998). A Primer of Abstract Mathematics.
- Joseph A. Gallian. (1990). Contemporary Abstract Algebra. Second Edition.
|
Here are a few quotes from Gallian that I enjoyed:
- "I agree with George Polya that guessing and conjecturing are important in mathematics and should be taught and encouraged wherever possible." [p. xi]
- "In my opinion, every undergraduate mathematics course should have a liberal arts character. I have tried to achieve this with comments, historical notes, quotations, biographies, and photographs, and in general, by my approach to the entire subject." [p. xi]
- "Several theorems are presented without proof. In each instance I feel that it is the understanding of the statement of the theorem, not its proof, that is the important issue." [p. x]
There are a number of issues to keep in mind as one Learns more about abstract algebra. One is to identify the theorems that appear to be the most important, and similarly, to identify the proofs that reveal the beauty of a proof. Another is to think of examples that illustrate the abstract theorems. Third, is to solve most of the exercises that are presented. Fourth, is to think of a few good questions about what one has Learned.
The zeroth chapter of the Gallian book is called Preliminaries [p. 3 - 20] |
Axiom: Well Ordering Principle
Every nonempty set of positive integers contains a smallest member.
This is self-evident. Think of any set of positive integers. For example {3,12, 2, 99}. Reorder the numbers from smallest to largest. Then the first number in the reordered set will be the smallest member. In this example, the reorderd set is {2, 3, 12, 99} and the smallest member is 2.
The principle also applies to any finite set of integers, positive, negative or zero, but it does not apply to the infinite set of all integers since there is no end to the number of negative integers and thus this set does not have a smallest number.
Definition: A nonzero integer t is a divisor of an integer s if there is an integer u such that s = tu.
Notation: In this case we write t | s and say "t divides s"
Definition: A prime is a positive integer greater than 1 whose only positive divisors are 1 and itself.
Theorem: Division Algorithm
Let a and b be integers with b > 0. Then there exist integers q and r with the property that a = bq + r where 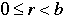 . .
Proof:
No |
Description |
Reason |
1 |
Consider the set S = {a - bk | k is an integer and 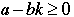 . . |
|
2 |
If 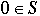 , then b divides a and we have q = a / b and r = 0. , then b divides a and we have q = a / b and r = 0. |
|
3 |
If 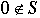 , and S is nonempty, then S has a smallest element, say r = a - bq , and S is nonempty, then S has a smallest element, say r = a - bq |
Well ordering principle |
4 |
Then a = bq + r and ... |
|
|
|
|
|
|
|
|
|
Mathematics 20
November 18
|
|
Mathematics Chronology |
8:40 am
This is a continuation of yesterday's note making while reviewing chapters 1 - 8 of "Fearless Symmetry". |
The book is divided into three main parts:
- Part One. Algebraic Preliminaries (chaps. 1 - 7)
- Part Two. Galois Theory and Representations (chaps. 8 - 16)
- Part Three. Reciprocity Laws (chaps. 17 - 23)
I am thoroughly enjoying this book. It is quite different than other books I have read in the last couple of years. I would categorize these books as follows:
- books that describe how to "do" certain things (e.g. textbooks)
- books on the history of mathematics
- general books on mathematics, but no "real" mathematics
- books that focus on the ideas and concepts of mathematics (this book!)
|
"Fearless Symmetry" is largely about terminology (i.e. concepts) and notation.
Let me try to review the previous seven chapters that constitute Part One:
Chapter |
Terminology (concepts) |
Description |
Notation |
| Part One |
Algebraic Preliminaries |
|
|
1 |
Representations |
|
|
|
set |
A set is a collection of things, often called the elements of the set. |
{a, b, c} |
|
one-to-one correspondence |
A one-to-one correspondence from a set A to set B is a rule that associates to each element in A exactly one element in B, in such a way that each element in B gets used exactly once, and for exactly one element in A. |
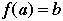
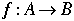
|
|
standard object |
This is an object that we know quite a bit about. |
|
|
function |
A function from a set A to a set B is a rule that assigns to each element in A an element of B. |
|
|
morphism |
A morphism is a function from A to B that captures at least part of the essential nature of the set A in its image in B. |
|
|
representation |
A representation is a morphism (i.e. a function) from a source object to a standard target object.
If A represents B, we have three things: two objects, A and B, which in this context will be sets, and the relation between them, which will be a morphism. When A and B have some additional "structure" (e.g. they are finite sets, or ordered sets, or ...) and we restrict the possible morphisms from A to B to have something to do with that structure. |
|
| |
Example:
Let A be the set {red, blue, yellow, pink}.
Let B be the standard object {1, 2, 3, 4}. Let f be the following rule: red is associated with 1, blue is associated with 2, yellow is associated with 3 and pink is associated with 4. f is a morphism because because this rule is capturing something about the number of elements in A. Therefore we may consider f to be a representation of A. |
2 |
Groups |
|
|
|
group |
A group G is a set with a composition defined on pairs of elements such that :
1. There is a neutral element e in G, so that 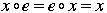 no matter what element in the group is substituted for x. e is sometimes called the identity element. no matter what element in the group is substituted for x. e is sometimes called the identity element.
2. For any element x of G, there is some element y in G so that 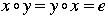 . That is, every element has an inverse element. . That is, every element has an inverse element.
3. For any three elements, x, y, and z in G, we have 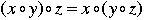 . This is called the associativity of the composition. Each group has its own law of composition. It can be whatever we define it to be (e.g. addition, multiplication, rotation, ...). . This is called the associativity of the composition. Each group has its own law of composition. It can be whatever we define it to be (e.g. addition, multiplication, rotation, ...). |
|
| |
group law |
If G is a group, the group law is the rule that tells how to combine two elements in the group to get the third. |
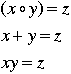 |
| |
discrete groups |
There is no smooth path from one element to another. (e.g. the integers under addition, permutation groups) |
|
| |
continuous groups |
There are infinitismal differences between elements. |
|
| |
Lie groups |
Pronounced "Lee", named after the Norwegian mathematician Sophus Lie who studied them. (e.g. rigid motions in space, rotations of a circle, rotations of a sphere, set of real numbers under addition) |
|
| |
Examples:
Consider the set Z of all the integers (positive, negative and zero). Z is an infinite set. Let the group law be familiar addition. Then Z under this group law is a group.
Consider the set of three rotations of 60, 120 and 180 degrees of an equilateral triangle. The rotations constitute the group law. The elements of the group are the three positions (i.e. orientations) of the triangle.
Groups are used to describe various types of symmetries. |
3 |
Permutations |
|
|
| |
permutation |
A permutation is a reordering of a set of elements. It is a function that assigns to each element of the set another element of the set such that it is a one-to-one correspondence. The function gives the rule for assigning each element. |
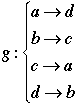 |
| |
group of permutations |
The collection of all possible permutation functions for a given set A forms a group. Notice that if A has n elements then 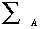 has n! elements. That is, there are n! different reorderings of n elements. has n! elements. That is, there are n! different reorderings of n elements. |
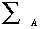 |
| |
identity permutation |
This is the function that leaves every element in the same position. |
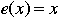 |
| |
inverse permutation |
This is the function that returns every element to its previous position. |
Let 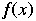 be a permutation of a set A. Then the inverse be a permutation of a set A. Then the inverse 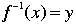 if and only if if and only if 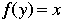 . . |
| |
cycle decomposition |
A particular permutation can be expressed as a series of cycles. For example, one such permutation of A = {a, b, c, d, e} may be a -> d -> a and b_> c -> e -> f-> c. |
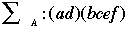 |
4 |
Modular Arithmetic |
Modular arithmetic is of fundamental importance in all of number theory. |
|
| |
conguence |
Congruence is a binary relation between two numbers similar to equality. Two numbers are said to be congruent modulo n if they have the same remainder when divided by n. |
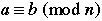 |
| |
modulus |
The number n that is the divisor is called the modulus of the congruence. |
|
| |
integer |
An integer is a whole number - positive, negative or zero |
|
| |
prime number |
A prime number is a positive integer greater than 1 that has no positive divisors except itself and 1. A negative number is also called prime if its absolute value is prime. |
|
| |
field |
A field is a number system where we can divide by anything nonzero. The integers modulo p (where p is a prime) are a field under addition and multiplication. We say that 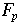 is a finite field with p elements. We also say that is a finite field with p elements. We also say that 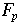 is a number system with characteristic p. Note that is a number system with characteristic p. Note that 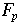 does not contain fractions. does not contain fractions.
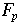 is a group under addition. is a group under addition.
If we delete the number 0 from 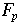 , we have a new set of p - 1 elements that is a group under multiplication. The new set is symbolized as "eff-pea-cross" : , we have a new set of p - 1 elements that is a group under multiplication. The new set is symbolized as "eff-pea-cross" : 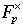 . . |
|
5 |
Complex Numbers |
|
|
| |
real number |
Any number that can be expressed as a decimal, either terminating or repeating. |
R |
| |
complex number |
A number of the form a + bi where a and b are real numbers. |
a + bi |
| |
complex conjugate |
A number of the form a - bi where a and b are real numbers. |
a - bi |
| |
set of all complex numbers |
|
C |
| |
Theorem |
Let 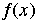 be a polynomial whose coefficients are any complex numbers. Then the equation be a polynomial whose coefficients are any complex numbers. Then the equation 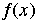 = 0 has solutions in C. = 0 has solutions in C. |
|
| |
algebraic closure |
The field C is closed under algebraic (i.e. addition, subtraction, multiplication, division, and the taking of roots) operations. This is a restatement of the previous theorem. |
|
| |
|
|
|
6 |
Equations and Varieties |
One of the main problems in number theory is finding and understanding all solutions of Z-equations. |
|
| |
rational number |
Any number that can be expressed at the ratio of two integers. |
|
| |
irrational number |
Any number that is not rational. |
|
| |
set of all rational numbers |
|
Q |
| |
Z-equation |
Also called a Diophantine equation. |
|
| |
set of all integers |
|
Z |
| |
set of integers modulo p |
|
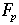 |
| |
variety |
The variety S defined by a Z-equation (or a system of Z-equations) is the function that assigns to any number system A the set of solutions S(A) of the equation.
Many different systems of equations can define the same variety S. |
S(A) |
| |
Fermat's Last Theorem |
For any positive integer n, let the variety 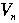 be defined by be defined by 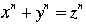 . Then if n > 2, . Then if n > 2, 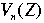 contains only solutions where one or more of the variables is 0. contains only solutions where one or more of the variables is 0.
It is easier to study 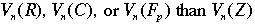 . Then some information about . Then some information about 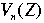 (the solution set we are really interested in) can be derived from the preceding three sets using advanced theorems from number theory and algebraic geometry. (the solution set we are really interested in) can be derived from the preceding three sets using advanced theorems from number theory and algebraic geometry. |
|
| |
roots of a polynomial |
If 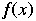 is a polynomial, the roots of is a polynomial, the roots of 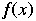 are those numbers c so that are those numbers c so that 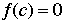 . . |
|
7 |
Quadratic Reciprocity |
|
|
| |
Legendre symbol |
|
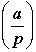 |
| |
Quadratic Recirocity |
|
Suppose that p and q are odd primes.
1. 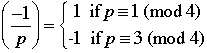
2. 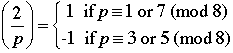
3. If 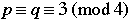 , then , then 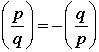 . .
4. If p or q or both 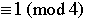 , then , then 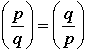 . . |
| Part Two |
Galois Theory and Representations |
|
|
8 |
Galois Theory |
|
|
| |
algebraic numbers |
A complex number is algebraic if it is the root of some Z-polynomial. |
|
| |
set of all algebraic numbers |
That subset of C which consists of all the equations 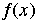 = 0 where = 0 where 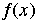 is a polynomial with integer coeficients. It can be shown that is a polynomial with integer coeficients. It can be shown that 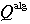 is a field. Note that i is an algebraic number (it is the solution to the equation is a field. Note that i is an algebraic number (it is the solution to the equation 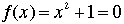 ). ).
Examples:
All the integers. (they are solutions for the polynomial equation x - n = 0 ).
All rational numbers. (they are solutions for the polynomial equation bx - a = 0 ).
nth roots of every fraction. ( they are solutions for the equation 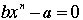 . . |
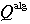 |
| |
algebraically closed field |
It can be shown that the sum, difference, product and quotient of any two algebraic numbers will also be an algebraic number.
p is not in 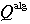 . (This is difficult to prove.) . (This is difficult to prove.)
It can be difficult to prove whether a particular number is or is not in 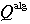 . .
There are lots of algebraic numbers and they are connected in many complicated ways. |
|
| |
absolute Galois group |
1. 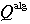 is the set of all complex numbers that can appear as roots of Z-polynomials. is the set of all complex numbers that can appear as roots of Z-polynomials.
2. The absolute Galois group G is made up of all permutations g of 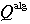 that preserve addition and multiplication. that preserve addition and multiplication.
3. If g is any element of G and f(x) is any Z-polynomial, then as g acts as a permutation of 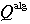 , it permutes the roots of f(x). It never maps some root of f(x) to a nonroot of f(x). , it permutes the roots of f(x). It never maps some root of f(x) to a nonroot of f(x).
4. G has infinitely many elements.
5. There is only one element of G, other than the neutral element e, for which we can give a complete description. This element is called c, the complex conjugate. No other element of G an be written down explicitly.
6. Any element g of G can be partially described by taking a Z-polynomial f(x), listing its roots 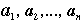 and telling what permutation of these algebraic numbers occurs when we apply g. and telling what permutation of these algebraic numbers occurs when we apply g.
7. Zorn's Lemma plus some advanced algebra can be used to piece together the partial descriptions of item 6 to get elements of G. That is how we know that G is infinite. |
G |
| |
Zorn's Lemma |
Allows us to compress the process of doing infinitely many things in a short amount of time, so that we can still have time left over. |
|
| |
symmetry |
A symmetry is a function that preserves what we feel is important about an object.
Each g in the Galois group G is a symmetry of 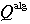 because it preserves the operations that concern us in algebra, namely, addition and multiplication. because it preserves the operations that concern us in algebra, namely, addition and multiplication. |
|
| |
|
|
|
Whew! But the above set of notes is a major step forward for me. I do not yet feel that I understand what a Galois group is or why it is important, but I do understand that it is a very important concept in modern algebra.
I have conducted a brief google of modern algebra textbooks and have identified two, which happen to be in the university library. Both are written by Joseph Rotman. One is called Advanced Modern Algebra and the second is called Theory of Groups. I want to have a look at them and see if they look accessible.
12:45 PM |
|
|
Mathematics 19
November 17
|
|
Mathematics Chronology |
2:30 PM
I have read and reread "Fearless Symmetry" chap 8 Galois Groups a few times during the last week. Now to make a few notes. |
The book is divided into three main parts:
- Part One. Algebraic Preliminaries (chaps. 1 - 7)
- Part Two. Galois Theory and Representations (chaps. 8 - 16)
- Part Three. Reciprocity Laws (chaps. 17 - 23)
I am thoroughly enjoying this book. It is quite different than other books I have read in the last couple of years. I would categorize these books as follows:
- books that describe how to "do" certain things (e.g. textbooks)
- books on the history of mathematics
- general books on mathematics, but no "real" mathematics
- books that focus on the ideas and concepts of mathematics (this book!)
|
"Fearless Symmetry" is largely about terminology (i.e. concepts) and notation.
Let me try to review the previous seven chapters that constitute Part One:
Chapter |
Terminology (concepts) |
Notation |
| Part One |
Algebraic Preliminaries |
|
1 |
Representations |
|
|
set |
|
|
one-to-one correspondence |
|
|
standard object |
|
|
function |
|
|
morphism |
|
|
representation |
|
2 |
Groups |
|
|
group |
|
| |
group law |
|
| |
discrete groups |
|
| |
integers under addition |
|
| |
permutation group |
|
| |
continuous groups |
|
| |
Lie groups |
|
| |
rigid motions in space
|
|
| |
rotations of a circle
|
SO(2) |
| |
rotations of a sphere
|
SO(3) |
| |
set of real numbers under addition |
R |
3 |
Permutations |
|
| |
group of permutations |
|
| |
identity permutation |
e |
| |
cycle decomposition |
|
4 |
Modular Arithmetic |
|
| |
conguence |
|
| |
modulus |
|
| |
integer |
|
| |
prime number |
|
| |
field |
|
5 |
Complex Numbers |
|
| |
real number |
|
| |
complex number |
a + bi |
| |
complex conjugate |
a - bi |
| |
set of all complex numbers |
C |
| |
algebraic closure |
|
6 |
Equations and Varieties |
|
| |
rational number |
|
| |
irrational number |
|
| |
set of all rational numbers |
Q |
| |
Z-equation |
|
| |
set of all integers |
Z |
| |
set of integers modulo p |
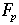 |
| |
variety |
|
| |
roots of a polynomial |
|
7 |
Quadratic Reciprocity |
|
| |
Legendre symbol |
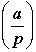 |
| |
Quadratic Recirocity |
Suppose that p and q are odd primes.
1. 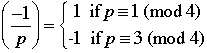
2. 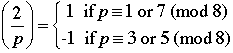
3. If  , then , then 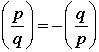 . .
4. If p or q or both 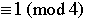 , then , then 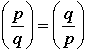 . . |
| Part Two |
Galois Theory and Representations |
|
8 |
Galois Theory |
|
| |
algebraic numbers |
|
| |
set of all algebraic numbers |
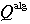 |
| |
algebraically closed field |
|
| |
absolute Galois group |
G |
| |
|
|
| |
|
|
I am not happy with the above table (yet). Although it identifies many of the important concepts that have been discussed so far, it fails to clarify exactly what these concepts are.
I need to add one more column that does this.
I also need to add at least one example to illustrate the nature of the concept. |
Chapter |
Terminology (concepts) |
Description |
Notation |
| Part One |
Algebraic Preliminaries |
|
|
1 |
Representations |
|
|
|
set |
A set is a collection of things, often called the elements of the set. |
{a, b, c} |
|
one-to-one correspondence |
A one-to-one correspondence from a set A to set B is a rule that associates to each element in A exactly one element in B, in such a way that each element in B gets used exactly once, and for exactly one element in A. |
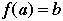
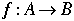
|
|
standard object |
This is an object that we know quite a bit about. |
|
|
function |
A function from a set A to a set B is a rule that assigns to each element in A an element of B. |
|
|
morphism |
A morphism is a function from A to B that captures at least part of the essential nature of the set A in its image in B. |
|
|
representation |
A representation is a morphism (i.e. a function) from a source object to a standard target object.
If A represents B, we have three things: two objects, A and B, which in this context will be sets, and the relation between them, which will be a morphism. When A and B have some additional "structure" (e.g. they are finite sets, or ordered sets, or ...) and we restrict the possible morphisms from A to B to have something to do with that structure. |
|
| |
Example:
Let A be the set {red, blue, yellow, pink}.
Let B be the standard object {1, 2, 3, 4}. Let f be the following rule: red is associated with 1, blue is associated with 2, yellow is associated with 3 and pink is associated with 4. f is a morphism because because this rule is capturing something about the number of elements in A. Therefore we may consider f to be a representation of A. |
2 |
Groups |
|
|
|
group |
A group G is a set with a composition defined on pairs of elements such that :
1. There is a neutral element e in G, so that 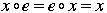 no matter what element in the group is substituted for x. e is sometimes called the identity element. no matter what element in the group is substituted for x. e is sometimes called the identity element.
2. For any element x of G, there is some element y in G so that 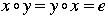 . That is, every element has an inverse element. . That is, every element has an inverse element.
3. For any three elements, x, y, and z in G, we have 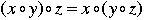 . This is called the associativity of the composition. Each group has its own law of composition. It can be whatever we define it to be (e.g. addition, multiplication, rotation, ...). . This is called the associativity of the composition. Each group has its own law of composition. It can be whatever we define it to be (e.g. addition, multiplication, rotation, ...). |
|
| |
group law |
If G is a group, the group law is the rule that tells how to combine two elements in the group to get the third. |
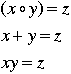 |
| |
discrete groups |
There is no smooth path from one element to another. (e.g. the integers) |
|
| |
integers under addition |
|
|
| |
permutation group |
|
|
| |
continuous groups |
There are infinitismal differences between elements. |
|
| |
Lie groups |
Pronounced "Lee", named after the Norwegian mathematician Sophus Lie who studied them. |
|
| |
rigid motions in space
|
|
|
| |
rotations of a circle
|
|
SO(2) |
| |
rotations of a sphere
|
|
SO(3) |
| |
set of real numbers under addition |
|
R |
| |
Examples:
Consider the set Z of all the integers (positive, negative and zero). Z is an infinite set. Let the group law be familiar addition. Then Z under this group law is a group.
Consider the set of three rotations of 60, 120 and 180 degrees of an equilateral triangle. The rotations constitute the group law. The elements of the group are the three positions (i.e. orientations) of the triangle.
Groups are used to describe various types of symmetries. |
3 |
Permutations |
|
|
| |
group of permutations |
|
|
| |
identity permutation |
|
e |
| |
cycle decomposition |
|
|
4 |
Modular Arithmetic |
|
|
| |
conguence |
|
|
| |
modulus |
|
|
| |
integer |
|
|
| |
prime number |
|
|
| |
field |
|
|
5 |
Complex Numbers |
|
|
| |
real number |
|
|
| |
complex number |
|
a + bi |
| |
complex conjugate |
|
a - bi |
| |
set of all complex numbers |
|
C |
| |
algebraic closure |
|
|
6 |
Equations and Varieties |
|
|
| |
rational number |
|
|
| |
irrational number |
|
|
| |
set of all rational numbers |
|
Q |
| |
Z-equation |
|
|
| |
set of all integers |
|
Z |
| |
set of integers modulo p |
|
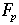 |
| |
variety |
|
|
| |
roots of a polynomial |
|
|
7 |
Quadratic Reciprocity |
|
|
| |
Legendre symbol |
|
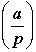 |
| |
Quadratic Recirocity |
|
Suppose that p and q are odd primes.
1. 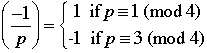
2. 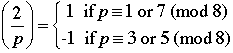
3. If 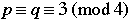 , then , then 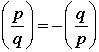 . .
4. If p or q or both 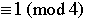 , then , then 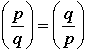 . . |
| Part Two |
Galois Theory and Representations |
|
|
8 |
Galois Theory |
|
|
| |
algebraic numbers |
|
|
| |
set of all algebraic numbers |
|
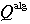 |
| |
algebraically closed field |
|
|
| |
absolute Galois group |
|
G |
| |
|
|
|
| |
|
|
|
|
|
Mathematics 18
November 11
|
|
Mathematics Chronology |
9:00 am
I read Ian Stewart's small book "Letters to a Young Mathematician" (2006) a couple of days ago and would like to capture a few of the sentences. |
Letters to a Young Mathematician (2006). Ian Stewart.
- "A typical day for the modern academic is ten or twelve hours long, with teaching commitments, research grants to pursue, research to be carried out, and liberal doses of pointless bureaucracy to get in the way of anything creative." [p. x]
- "Our society consumes an awful lot of math, but it all happens behind the scenes. The reason is straightforward: that's where it belongs." [p. 2]
- "So each conversation is broken up into thousand upon thousands of short pieces, and only one piece in a hundred is actually transmitted. At the other end, the missing ninety-nine pieces are restored by filling in the gaps as smoothly as possible." [p. 5]
| Fascinating. I didn't realize that we didn't send all of the packets. I thought I was reading a math book and I end up Learning more about the Internet. |
- "What math does for me is this: It makes me aware of the world I inhabit in an entirely new say. It opens my eyes to nature's laws and patterns. It offers an entirely new experience of beauty." [p. 7]
- "Some people think that this kind of understanding 'spoils' the emotional experience. I think this is rubbish. It demonstrates a depressing sort of aesthetic complacency. ... they suffer from a serious lack of curiousity: they refuse to believe the world is more wonderful than their own limited imaginations." [p. 8]
- "When I look at a crystal, I am aware of the beauties of its atomic lattice as well as the charm of its colors." [p. 9]
- "Then there's the inner beauty of mathematics, which should not be underrated. Math done 'for its own sake' can be exquisitely beautiful and elegant." [p. 9]
- "So he spent all of his free periods teaching us extra math, outside of the syllabus. During the regular math lessons he told us to sit at the back and do our homework; not just math, any homework. And to shut up. Those lessons weren't for us; we had to give the others a chance." [p. 14]
- "An awful lot of what is now called 'mathematics' at school is really arithmetic. ... 'Modern' is a strange word to use here: it means between one and two hundred years old, as opposed to the two-hundred years old math that formed the bulk of the older syllabus." [p. 19]
- "At university you will encounter a much broader conception of mathematics. ... You may learn how the great mathematicians of the Renaissance solved cubic and quartic equations ... if so, you will probably find out why such methods fail for quintic equations. You will see why this becomes almost obvious if you ignore the numerical values of the equations' solutions and instead think about their symmetries, and why it is arguably more important to understand the symmetries of equations thatn to be able to solve them." [p. 20]
| This is exactly what I am reading about at the moment in both "The Equation That Couldn't Be Solved" and in "Fearless Symmetry". |
- "... you will find that you can recognize mathematics when you see it, but you still can't define it. Which is as it should be. Definitions pin thing s down, they limit the prospects for creativity and diversity. ... Math, like anything still under development, always has the potential to surprise." [p. 22]
- "Our brains are not like computers, working systematically and logically. They are metaphor machines that leap to creative conclusions and belatedly shore them up with logical narratives." [p. 23]
- "Or, as my friend David Tall often says, 'Math is not a spectator sport.' " [p. 24]
- "Math is not a robotic way of replacing thought by rigid ritual. It is the most creative activity on the planet." [p. 33]
- "Why do so many people think that their school textbook contains every possible question?" [p. 34]
- Locate "To Talk of Many Things" by Dame Kathleen Ollerenshaw. [p. 35]
- "... the texts do not ask questions that the methods being taught cannot answer. So, isidiously, we absorb the lesson that every mathematical question has an answer. It's not true." [p. 37]
- "When you study any subject, the rate at which you can understand new material tends to accelerate the more you already know." [p. 39]
- "... pretty much everything that students are exposed to boils down to buttons you could push on a pocket calculator." [p. 40]
- "Questions ... are important because our efforts to find the answer reveal major gaps in our understanding of mathematics." [p. 43]
- "But math is not about sums, not really. It's about patterns ad why they occur. Nature's patterns are both beautiful and inexhaustible." [p. 46]
- "... ideas in mathematics seem to arise in three stages: ... preparation ... incubation followed by illumination ... verification." [p. 54 - 55]
- "You need to understand how to learn." [p. 63]
- "Many students believe that if you get stuck, you should stop. ... I always tell my students that the first thing to do is read on. ... Often the next sentence, or the next paragraph, will resolve your problem." [p. 64]
- "If you are still stuck ... now is the time to ... ask for assistance." [p. 65]
- "Whenever you get stuck on a piece of mathematics, it usually happens because you do not properly understand some other piece of mathematics, which is being used without explicit mention on the assumption that you can handle it easily." [p. 65]
- "Read around your subject. Do not read only the assigned text. ... Find some books on the same topic or similar topics. Read them, but in a fairly casual way." [p. 67]
- "Microscopes made biology more interesting, not less, by opening up new ways to approach the subject. It's the same with computers and mathematics." [p. 82]
- "Computer-assisted proofs raise issues of taste, creativity, technique, and philosophy." [p. 106]
- "It's fine for people to advocate their point of view on how math should be done. But they should not presume that there is only one good way to do math. I prefer diversity." [p. 140]
- "You should use the tools at hand, adapt and modify them to suit your own projects, and make new ones as the need arises." [p. 146]
- "I read a lot, often in fields unrelated to my own, and my best ideas often come when something I have read reminds me of something I already know about." [p. 153]
| This describes me to a T. |
- "We now have a highly prescriprive 'national curriculum', and teachers - quite literally - check hundreds of boxes to mark the student's progress. ... The assumption is that what really matters is their ability to get the answer. But what really matters is how they get the answer. ... I am absolutely certain that checking a series of boxes is not the way to teach anyone mathemtics." [p. 167]
2:40 PM Now to return to "Fearless Symmetry" and quadratic reciprocity.
The authors make a special point of highlighting the importance of a good notation and how that may guide thinking. They mention the Legendre symbol as a case in point.
Here is the notation: 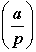
What does it mean? At least in the present context it refers to a pattern related to solutions to the equation 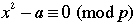 . This quadratic equation will have either 0, 1 or 2 solutions depending on the values of a and p. . This quadratic equation will have either 0, 1 or 2 solutions depending on the values of a and p.
The Legendre symbol gives the values of -1, 0 or 1 depending on the number of solutions. Amazingly, this function has a number of interesting properties. For example:
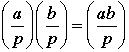
Theorem 7.2
Let a be a positive integer.
1. If p and q are two odd primes so that 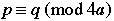 , then , then 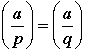 . .
2. If p and q are two odd primes so that 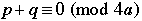 , then , then 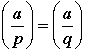 . .
It turns out that this is difficult to prove, but we can use the result and continue.
Theorem 7.3 (Quadratic Reciprocity)
Suppose that p and q are odd primes.
1. 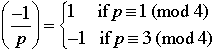
2. 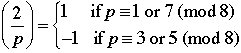
3. If  . .
4. If p or q or both are 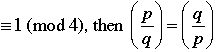 . .
Why do we care about all of this? Because we can use these results to compute Legendre symbols for large numbers by using the known values for much smaller numbers and this is a way of knowing whether certain quadratic equations have 0, 1 or 2 solutions, without actually having to find the solutions. From a practical point of view one may view this as an improvement, or maybe not (who cares about quadratic equations anyway). Alternatively, there is something very beautiful and magical about being to do this. Now it is possible to know if certain quadratic equations have a solution without actually having to find it. From the point of view of logic this is indeed very cool.
3:30 PM |
|
|
Mathematics 17
November 8
|
|
Mathematics Chronology |
8:10 am
I am back to chapter 7 of "Fearless Symmetry" which is on the idea of quadratic reciprocity.
This is an introduction to the general idea of looking at groups of Z-equations (i.e. equations with integral coefficients). The chapter restricts itself to the simplest types of interesting Z-equations, namely quadratic equations. Furthermore it restricts the solutions to those in the field 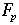 , for various prime numbers p. , for various prime numbers p. |
Fearless Symmetry (2006). Avner Ash & Robert Gross.
Chapter 7 Quadratic Reciprocity [p. 67 - 83]
- "... quadratic reciprocity is the tip of the gigantic iceberg of 'reciprocity laws' ... [p. 68]
- One might begin with equations of degree 1, that is, equations of the form ax + b = 0. For any field R, the solution set is simply the element -b/a which is always defined since we are working within a field.
- The next most difficult case is that of the quadratic. The general form of a quadratic equation is
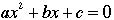 . But rather than start with this case, we will deal with the simpler situation . But rather than start with this case, we will deal with the simpler situation 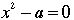 . .
- If a is 0, then the solution set will be x = 0, that is, it will contain just one number, 0.
- If a is 1, then the solution set S(Z) = {1, -1}. Also S(Q), S(R) and S(C) are the same set {1, -1}.
- If a is -1, then the solutions sets S(Z), S(Q) and S(R) are all the empty set, but S(C) = {i, -i}.
- In general the solution set for the equation
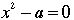 will contain either no elements or two elements (when a is a perfect square). will contain either no elements or two elements (when a is a perfect square).
- Staying with the same equation
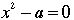 , we will now have a closer look at the field , we will now have a closer look at the field 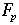 for different values of the prime number p. for different values of the prime number p.
Pedagogically, the authors have done a superb job of introducing this idea beginning with the simplest possible case and then slowly and meticulously extending it to more complex and interesting cases. This is also a great example of how new mathematics is actually done! |
- Begin with a = 1. Consider the polynomial
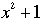 , or equivalently, the equation , or equivalently, the equation 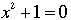 . Now examine various values of p, beginning with p = 3. . Now examine various values of p, beginning with p = 3.
- if x = 0, we have
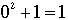 which is not congruent to 0 modulo 3 (Note: being congruent to 0 modulo p is equivalent to saying that this value is a root of the equation). which is not congruent to 0 modulo 3 (Note: being congruent to 0 modulo p is equivalent to saying that this value is a root of the equation).
- if x = 1, we have
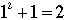 which is not congruent to 0 modulo 3. which is not congruent to 0 modulo 3.
- if x = 2, we have
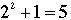 which is not congruent to 0 modulo 3. which is not congruent to 0 modulo 3.
- Therefore there are no solutions to the equation. Notationally,
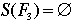 . .
- Consider next the various values of the polynomial when p = 5. It is easy to verify that
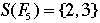 . Similarly one can work out values for other values of p. After a while one may notice that when . Similarly one can work out values for other values of p. After a while one may notice that when 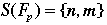 , it is also true that n + m = p. , it is also true that n + m = p.
- Thus we have shown that the solution set
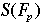 may have 0, 1 or 2 elements modulo p. may have 0, 1 or 2 elements modulo p.
- Legendre created the notation
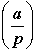 to represent the number of solutions to to represent the number of solutions to 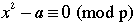 where: where:
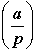 = -1 if = -1 if 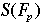 contains no elements contains no elements-
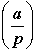 = -0 if = -0 if 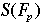 contains 1 element contains 1 element
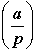 = 1 if = 1 if 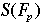 contains 2 elements. contains 2 elements.
At first this may seem a bit strange, if not simply arbitrary. However this notation allows one to "see" certain patterns that would otherwise be very difficult to notice. [p. 73]
|
|
Mathematics 16
November 6
|
|
Mathematics Chronology |
8:00 PM
I have finished reading "The Equation that Couldn't be Solved". Stunning! This is an amazing book. The variety of examples of how symmetry is a part of our life reads like a renaissance document. The detailed biography of Galois' life is fantastic. As a motivator to learn more about group theory the book is without peer. However the book is deliberately light on the actual mathematics underlying both symmetry and group theory. This is where "Fearless Symmetry" shines.
Now that I have finished reading the book, the question arises, "Should I make some notes about this, and if so, how?"
I think I will begin by noting some of the yellow highlighted sentences. |
The Equation That Couldn't Be Solved (2005). Mario Livio
Chapter 1 Symmetry [p. 1 - 28]
- "I hope that the story as a whole will depict both the humanistic side of mathematics and, even more importantly, the human side of mathematicians." [p. 2]
- "Yet group theory, the mathematical language that describes the essence of symmetries and explores their properties, did not emerge form the study of symmetries at all." [p. 2 - 3]
- "Bilateral symmetry is so prevalent in animals that it can hardly be due to chance." [p. 6]
- "... all directions on the surface of the Earth are not created equal. A clear distinction between up and down ... is introduced by the Earth's gravity." [p. 6]
- "Having all the sensory organs ... in the front clearly helps the animal in deciding where to go and how best to get there." [p. 6]
- "There is nothing major in the sea, on the ground, or in the air, to distinquish between left and right." [p. 7]
- "... many multicellular animals have an early embryonic body that lacks bilateral symmetry. The driving force behind the modification of the 'original plan' as the embryo grows may indeed be mobility. ... Life forms that are anchored in one place and are unable to move voluntaraily, such as plants and sessile animals, do have very different tops and bottoms, but no distinquishable front and back or left and right." [p. 7]
- "Any civilization sufficiently evolved to engage in interstellar travel has likely long passed the merger of an intelligent species with its far superior computational-technology-based creatures. A computer-based super-intelligence is most likely to be microscopic in size." [p. 8]
- "Have nothing in your houses which you do not know to be useful or believe to be beautiful." [p. 17]
- "The arts and sciences are chock-full of fascinating examples of symmetry under the operations of translation, rotation, reflection, and glide reflection ..." [p. 22]
- "An interesting transformation that is not geometrical in nature involves permutations - the different rearrangement of objects, numbers, or concepts." [p. 22]
- a = b is symmetric under the interchange of a and b, but a < b is not symmetric under such an interchange. [p. 23]
- roulette is an example of a game that is symmetric with respect to the players - everyone has the same chance of winning. Blackjack is an example of a game that is not symmetric with respect to the players - good strategy is important. [p. 24 - 25]
Chapter 2 The Mind's Eye in Symmetry [p. 29 - 50]
- "To the Gestalt psychologists, therefore, symmetry was one of the key elements to contributing significantly to the 'goodness' of the figure." [p. 34]
- "Two other important elements in the Gestalt principles of organization are proximity and similarity." [p. 35]
- "Symmetry plays an important role in the recognition of similarity because it represents a true invariant - an immunity to change." [p. 35]
- "Humans have been 'practicing' perception for generations, and through their endless number of perceptual encounters they have learned what to expect." [p. 37]
- "With every step toward the revolutions of relativity and quantum mechanics, the role of symmetry in the laws of nature has become increasingly appreciated." [p. 43]
- "A group ... is a set that has to obey certain rules with respect to some operation. ... The properties that define a group are"
- closure
- associativity
- identity element
- inverse.
... this simple definition can lead to a theory that embraces and unifies all the symmetries of our world." [p. 46]
Chapter 3 Never Forget This in the Midst of Your Equations [p. 51 - 89]
- "Concern for man himself and his fate must always constitute the chief objective of all technological endeavors ... in order that the creations of our mind shall be a blessing and not a curse to mankind. Never forget this in the midst of your diagrams and equations." (Albert Einstein) [p. 51]
- "Diophantus is best known today for a special class of equations that bears his name - Diophantine equations." (these are sets of equations that have integral solutions) [p. 59]
- "Muhammad ibn Musa al-Khwarizmi (ca. 780 - 850) ... was the first to expose in a systematic way the solutions of quadratic equations." [p. 61]
- "... the solution to the general cubic (and quartic) equation defied mathematicians until the sixteenth century." [p. 63]
- "Lagrange made the important discovery that the properties of equations and their solubility depend on certain symmetries of the solution under permutations." [p. 84]
- "Gauss gave his first proof of what has become known as the fundamental theorem of algebra - the statement that every equation of degree n has precisely n solutions. ... The fundamental theorem demonstrated unambiguously that the general quintic equation must have five solutions. But could these be found by a formula?" [p. 85]
- "This was the setting into which two young men, perhaps the most tragic figures in the history of science, appeared. The Norwegian Niels Henrik Abel and the Frenchman Evariste Galois were about to change the course of algebra forever." [p. 89]
Chapter 4 The Poverty-Stricken Mathematician [p. 90 - 111]
- an excellent biography of Abel.
Chapter 5 The Romantic Mathematician [p. 112 - 157]
- a superb biography of Galois.
Chapter 6 Groups [p. 158 - 197]
- In addition to the general concept of a permutation, are the related ideas of even and odd permutations (depending on the number of reversals of the elements). [p. 161]
- Another important idea is the idea of a cyclic permutation [p. 163]
- "Galois ... discovered an ingenious way to determine whether an equation is solvable from an examination of the symmetry properties of permutations of its solutions." [p. 163]
- "The identification of permutations as crucial mathematical objects worthy of study thus set Galois on the road to formulating group theory." [p. 164]
- "Permutations and groups are intimately related." [p. 164]
- "... two groups that have the same structure or the same 'multiplication table', such as the group of permutations of three objects and the group of symmetries of the equilateral triangle, are called isomorphic." [p. 167]
- "... certain subsets of the members of a group may by themselves satisfy all the four requirements of being a group (closure, associativity, identity, inverse). In that case the subset is said to form a subgroup." [p. 168]
- "If we divide the order (number of members) of the parent group ... by the order of the subgroup ... we obtain the composition factor." [p. 168]
- "An important theorem due to Lagrange ... The order of a finite subgroup always evenly divides the order of its finite parent group." [p. 168]
- "Galois started by showing that every equation has its own 'symmetry profile' - a group of permutations (now called the Galois group) that represents the symmetry properties of the equation. ... Before Galois, equations were always classified only by their degree: quadratic, cubic, quintic, and so on. Galois discovered that symmetry was a more important characteristic." [p. 170]
- "Galois was able to prove that for any degree n, one can always find equations for which the Galois group is actually the full permutation group. In other words, he showed that for any degree, there are equations that possess the maximum symmetry possible." [p. 170]
- "Galois then defined a normal subgroup. If any member of a subgroup satisfies the property that multiplying it from the left by a member of the parent group and from the right by the inverse gives a member of the subgroup, then the subgroup is called a normal subgroup." [p. 171]
- "Galois called a group solvable if every single one of the composition factors generated by its descendent maximal subgroups was a prime number. ... the condition for an equation to be solvable by a formula is that its Galois group should be solvable." [p. 171]
The remainder of the book returns to the theme of the first three chapters where a large variety of examples of symmetry in various scientific, artistic and psychological endeavors.
The concept of a normal subgroup seems to appear out of thin air. Where did this particular combination come from?
I still do not "fully" understand Galois' proof, but I do feel that I have a general sense of what he acomplished and definitely realize that group theory is an incredibly important branch of mathematics.
I can hardly wait until tomorrow when I hope to return to "Fearless Symmetry". |
10:00 PM
|
|









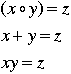
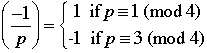
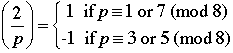
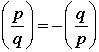 .
.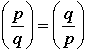 .
.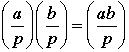
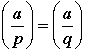 .
.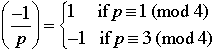
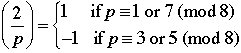
 .
.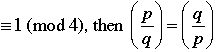 .
.